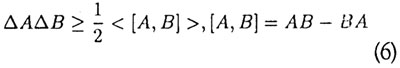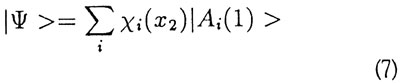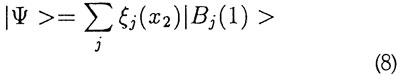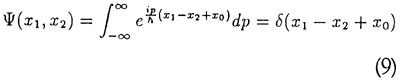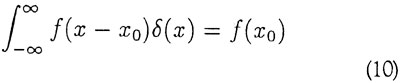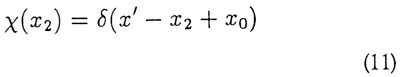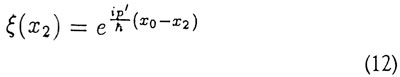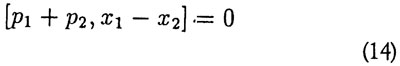|
|
EINSTEIN-PODOLSKY-ROSEN-PARADOKSET
- af Carsten Agger
oprindelig bragt i Tidsskriftet Elsebeth nr. 11, 1995
Denne artikel omhandler det såkaldte Einstein-Podolsky-Rosen-Paradoks, med hovedvægten lagt på gennemgangen af forfatterens oprindelige argument og af Bohrs svar herpå.
Einstein, Podolsky og Rosen beviste i deres artikel fra 1935, at kvantemekanikken i følge sin egen formalisme er ufuldstændig: den samme fysiske virkelighed kan beskrives af to forskellige bølgefunktioner, der er egenfunktioner for to ikke-kommuterende observable. Dette er i modstrid med kvantemekanikken, der derfor må afløses af en mere fuldstændig teori.
Denne holdning deles stadig af mange mennesker, også (en minoritet blandt) fysikere. I artiklen gennemgås omhyggeligt EPR's oprindelige argument og Niels Bohrs tilbagevisning heraf. Bohr viste ved et eksempel, at de omtalte to forskellige bølgefunktioner repræsenterer to forskellige måleprocedurer, der gensidigt udelukker hinanden.
EPR-paradokset hører til de emner fra fysikken, der oftest behandles i den populærvidenskabelige litteratur, og er vel det, der oftest misforstås. Specielt går forfatterne som regel let hen over Bohrs svar eller slår det direkte hen som "uforståeligt". Dette er, som vi skal se, ikke rigtigt.
1. Kvantemekanikkens grundbegreber og fortolkning
1.1 Formalismen
I ikke-relativistisk kvantemekanik beskrives en partikel ved en bølgefunktion ψ (r,t), der opfylder Schrödingers ligning:
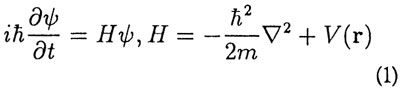
Bølgefunktionen kan også opfattes som en vektor | ψ > i et Hilbertrum. Fysiske størrelser repræsenteres så af observable, der er hermiteske mht. skalarproduktet
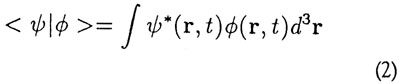
Et vigtigt postulat er det, at en måling af en fysisk størrelse kun kan resultere i en egenværdi for dennes repræsenterende operator. Antag, at vi ønsker at måle en given størrelse F (repræsenteret ved operatoren F), mens vores partikel er i tilstanden | ψ >. Hvad er vi nu i stand til at sige om resultatet af denne måling? For at svare på dette spørgsmål opløses | ψ > i egenvektorer for F:
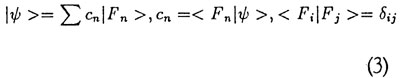
hvor vores | Fn > opfylder

Den almindelige fysiske fortolkning af ovenstående bygger på følgende regler:
Sandsynligheden for at få værdien fn som resultat af målingen er givet ved | cn | 2 = | < Fn | ψ > | 2 Dette kaldes Borns fortolkning. Men hvordan ser bølgefunktionen nu ud efter målingen? Ja, vores måling gav resultatet fk, og målinger postuleres nu (ideelt set) at kunne gentages med samme resultat, så vores system efter målingen beskrives af en tilstand ψ', der opfylder
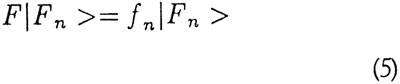
dvs. tilstanden er blevet projiceret ind på egenvektoren hørende til den målte egenværdi. Denne opførsel kaldes reduktion af bølgepakken eller (mere farverigt) "collapse of the wave function". Et systems tilstand er fuldstændigt beskrevet ved dets bølgefunktion.
Suppleret med den sædvanlige kvantisering 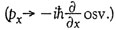 sætter dette os i stand til at komme med mangfoldige forudsigelser om mikroskopiske systemer, som bekendt med stor succes. sætter dette os i stand til at komme med mangfoldige forudsigelser om mikroskopiske systemer, som bekendt med stor succes.
En i denne sammenhæng specielt relevant konsekvens af den matematiske formalisme er, at to operatorer kun kan have fælles egentilstande, hvis de kommuterer, og det vil i følge fortolkningen sige, at de tilhørende fysiske størrelser ikke samtidig kan have en bestemt værdi; dette udtrykkes mest præcist ved ubestemtheds-relationen:
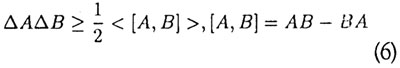
Som vi senere skal se, sætter disse relationer grænser ikke (alene) for den nøjagtighed hvormed sådanne par af fysiske størrelser kan kendes, men også for den nøjagtighed, hvormed de overhovedet kan defineres.
2. EPRs argument
EPR søger i deres artikel at vise, at kvantemekanikken ikke kan give en fuldstændig beskrivelse af den fysiske virkelighed. De mener, at man i hvert fald må stille to krav til en fysisk teori:
Korrekthed, det vil sige overensstemmelse mellem teoriens forudsigelser og de erfaringer, man kan gøre (via observationer, eksperimenter, ...) Fuldstændighed, det vil sige, at "alt hvad der findes i den fysiske virkelighed skal også findes i teorien".
Det sidste punkt udtrykker EPR som, at hvert element af den fysiske virkelighed skal have sit modstykke i teorien, hvor et sådant element defineres ved følgende kriterium:
Hvis man uden på nogen måde at forstyrre et system med sikkerhed (det vil sige, med sandsynlighed een) kan forudsige værdien af en fysisk størrelse, så findes der et element af fysisk virkelighed svarende til denne størrelse.
Kvantemekanikkens ufuldstændighed bliver nu en konsekvens af følgende argumentation: Hvis to fysiske størrelser (fx A og B) repræsenteres af operatorer, der ikke kommuterer, har de ingen fælles egentilstande. Dette betyder, at hvis det betragtede system er i en egentilstand for A ("værdien af A er kendt"), har det ingen mening (i kvanteteorien) at tillægge det nogen værdi for B. Dette vil også sige: Kan vi i en given tilstand forudsige værdien af to ikke-kommuterende operatorer, må kvanteteorien være ufuldstændig. EPR udtrykker det præcist ved to punkter:
Kvantemekanikkens beskrivelse af virkeligheden er ufuldstændig, eller hvis operatorene svarende til to fysiske størrelser ikke kommuterer, kan de to størrelser ikke samtidig være veldefinerede.
Antag, at vi har en situation, hvor et system, der (i een dimension) beskrives af bølgefunktionen ψ(χ1, χ2, t), splittes i to systemer (1) og (2), så det samlede system stadig er beskrevet ved ψ. Ønsker man nu at måle en fysisk størrelse A i systemet (1), må vi opløse ψ i egenvektorer for A(l) efter forskriften (3):
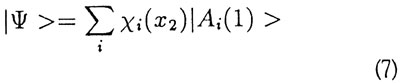
Måler vi i stedet en anden størrelse B i systemet (1), fås tilsvarende
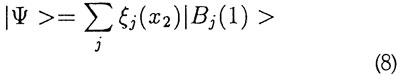
Måler vi altså A i system l (det vil sige A(l)) får vi et resultat ak, måler vi B(l), kan vi få resultatet bl. Samtidig vil system 2's tilstand efter målingen være enten | χk > eller | ξ1 >. Nu kan tilsyneladende den samme fysiske tilstand (system 2 efter målingen) beskrives ved to forskellige bølgefunktioner. Lader man specielt de to systemer være to partikler, A være deres position χ, B deres impuls ρ, kan man vælge
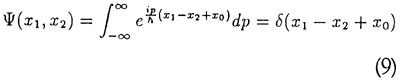
hvor δ er Diracs deltafunktion, defineret ved
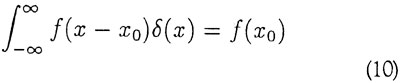
Måles nu χ1 med resultatet χ' + χ0 fås jf. (7)
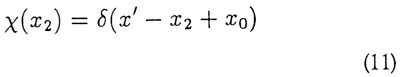
så partikel 2 nu er i en egentilstand for χ med værdien χ' + χ0. Vælger vi i stedet at måle ρ1 med resultatet ρ' fås omvendt
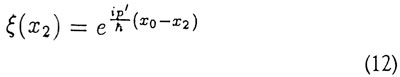
svarende til egenværdien -ρ' for ρ2. Da målingerne på partikel l i følge EPR ikke medfører nogen påvirkning af system 2, konkluderer EPR, at der i denne situation findes et element af fysisk virkelighed svarende til såvel ρ2 som χ2. Men så må - som ovenfor anført - den kvantemekaniske beskrivelse være ufuldstændig og bør afløses af en mere fuldstændig teori.
3. Bohrs argument
Det fortælles, at Niels Bohr efter offentliggørelsen af EPRs artikel straks lagde alt andet arbejde til side for at rette denne misforståelse. Kort efter kom der da også et svar, hvor han imødegik argumentet ved et eksempel, hvor det viser sig, at de to bølgefunktioner, der tilsyneladende begge beskriver et systems tilstand, er udtryk for to hinanden gensidigt udelukkende eksperimentelle procedurer; selv om der ikke kan være tale om, at målingen på eet system direkte, mekanisk påvirker det andet system, påvirker den selve de betingelser, der overhovedet tillader os at definere de pågældende fysiske størrelser. Denne formulering fandt fysikeren J.S. Bell (der er kendt for at have opstillet Bells ulighed) så kringlet og kryptisk, at han flot imødegik hele Bohrs argumentation ved at håne denne ene sætning. Lad i stedet os andre, der ønsker at gennemgå denne argumentation, begynde med at betragte konsekvenserne af at bruge det samme måleinstrument til at måle to ikke-kommuterende fysiske størrelser.
3.1 Målinger - et eksempel
Fysiske størrelser skal kunne defineres operationelt, dvs. som målelige størrelser. Lad os for at belyse problemerne i forbindelse med valget af måleprocedure se på en meget simpel kollision: En partikel passerer igennem en enkelt spalte i en skærm (Fig.l).
Dette simple eksempel illustrerer alle problemer ved måling af position og impuls. Skærmen betragtes i det følgende som et enkelt måleinstrument, der kan indgå i en større eksperimental opstilling. Det kan antages, at partiklens impuls før den passerer gennem spalten er fuldstændig kendt. Diffraktionen i spalten vil give en usikkerhed Δρ i partiklens impuls umiddelbart efter kollisionen; denne usikkerhed er forbundet med usikkerheden Δχ på partiklens stedkoordinat ved usikkerhedsrelationen, i dette tilfælde skrevet og fortolket som en ubestemthedsrelation:

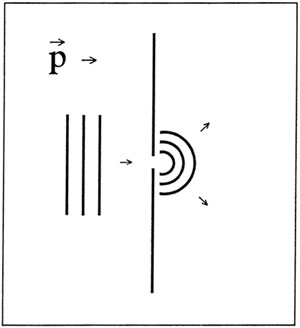
Figur 1.
Den således introducerede usikkerhed Δρ er forbundet med en udveksling af impuls mellem partiklen og skærmen. I hvilken udstrækning er det nu muligt at tage denne udveksling i betragtning? Vi ser på to mulige tilfælde:
Skærmen antages først at være spændt fast til resten af opstillingen på et fast underlag, der definerer koordinatsystemet (Fig.2). Den udvekslede impuls vil nu absorberes af dette underlag, og vi er således helt afskåret fra at tage den i betragtning ved forudsigelser om eksperimentets videre forløb.
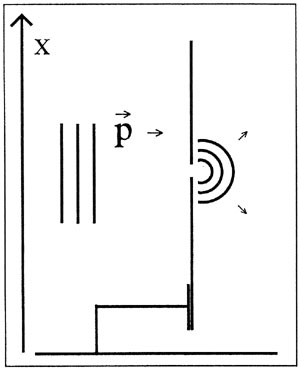
Figur 2: Opstilling, der muliggør kontrol af partiklens begyndelsesposition
Nu tænkes skærmen ikke fastspændt til underlaget, men i stedet ophængt på en sådan måde, at dens impuls kan måles før og efter partiklen passerer (Fig.3). Det er nu muligt ved impulsbevarelse at forudsige partiklens impuls efter kollisionen; omvendt må vi opgive en nøjagtig bestemmelse af skærmens (og dermed partiklens) position, idet den passerer.
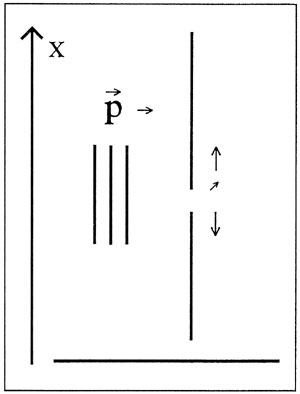
Figur 3: Opstilling, der muliggør forudsigelse af partiklens impuls
Skærmen kan bruges til at fastlægge begyndelsesbetingelserne for en partikel i forbindelse med en opstilling som i figur 4, hvor partiklen sendes ind mod en skærm med flere spalter for til sidst at blive registreret på en fotografisk plade.
I tilfældet 1) ovenfor kan skærmen bruges til at fastlægge begyndelsespositionen; gentages eksperimentet et stort antal gange, vil der på den fotografiske plade dannes et interferensmønster ud fn de sædvanlige betingelser.
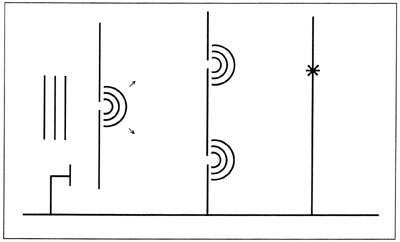
Figur 4: Skærm som før, her brugt til at kontrollere begyndelsesbetingelserne i et dobbeltspalteeksperiment
I tilfælde 2) kan skærmen derimod ikke bruges til at måle position med, eftersom en nøjagtig måling af skærmens impuls betyder, at relationen (13) må tages i betragtning ved overvejelser over dens position. Især gælder det, at hvis partiklens impuls kendes med tilstrækkelig nøjagtighed til at forudsige, hvilken spalte den vil passere igennem, vil usikkerheden på dens begyndelsesposition fuldstændig ødelægge interferensmønstret.
Desuden gælder i tilfælde 2), at efter den første måling af skærmens impuls kan man frit vælge, om man (efter kollisionen med partiklen) vil måle dens position (og herved fastlægge partiklens begyndelsesposition) eller dens impuls (og herved fastlægge partiklens impuls).
Men nu må vi ikke tabe ubestemthedsrelationen (13) af syne; for måler vi skærmens position, vil den herved udvekslede impuls som før absorberes af underlaget, og vi er helt afskåret fra at forudsige noget om partiklens impuls; for denne kan vi kun her definere (som målelig størrelse) ud fra impulsbevarelsessætningen, og absorptionen af en ukontrollabel impuls i vores underlag (id est, vores referencesystem) ødelægger hele grundlaget for at bruge denne på skærmpartikel-systemet. Omvendt vil målingen af skærmens impuls, som vi har set, fjerne ethvert grundlag for en meningsfuld definition af partiklens position i forhold til vort referencesystem. Bohr kaldte dette forhold komplementaritet: at størrelser som position og impuls, der er nødvendige for at beskrive alle aspekter af fysiske systemer og processer, dog ikke kan defineres samtidigt.
Man kan sætte situationen på spidsen ved at antage, at vi har 1000 fuldstændig identiske sådanne systemer. Straks efter, at alle partikler har ramt deres fotografiske plade, har vi to muligheder: Enten måler vi alle skærmenes impulser, og er nu i stand til at sige, hvilken spalte samtlige partikler passerede igennem; eller vi kan måle positionen af hver enkelt skærm og dermed kende hver enkelts begyndelsesposition. I det første tilfælde kan vi sortere alle disse stykker fotopapir (som vi i mellemtiden har fået fremkaldt) efter, hvilket hul partiklen passerede igennem, og kan betragte fordelingen svarende til partikler, der er blevet skudt ind mod et enkelt hul. I det andet tilfælde kan vi sortere dem efter begyndelsespositionen og vil herved få et interferensmønster svarende til diffraktion af bølger i begge spalter; vi har nu ingen ret til at tale om, hvorvidt en partikel er gået igennem den ene eller den anden spalte.
Det skulle nu være slået fast, at den måling, der i vores opstilling tillader os at bestemme partiklens impuls, langt fra at indebære nogen mekanisk forstyrrelse (her: forskydning) af partiklen påvirker det grundlag, hvorpå vi ville bygge en forudsigelse af dens position. Hvad mere er, det er netop denne påvirkning, der i kvanteteorien udtrykkes (eller: tages højde for) ved de tilsvarende operatorers manglende kommuteren.
3.2 EPRs eksempel
Man kan begynde med at bemærke, at EPR i deres eksempel udnytter, at
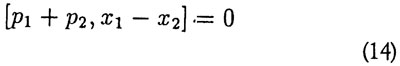
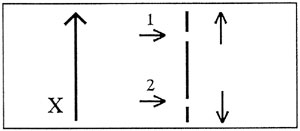
det vil sige, de opstiller en tilstand, der er egentilstand for både χ1 - χ2 og ρ1 + ρ2. Nøjagtig det samme kunne opnås ved en opstilling som i fig.5: to partikler sendes ind mod en skærm med to spalter, der er meget smalle i forhold til afstanden mellem dem. Hvis vi måler skærmens impuls både før og efter kender vi både
 |
|
Fig. 5.
|
Præcis som før kan vi nu måle den ene partikels position, det vil sige den kan fastlægges i forhold til et instrument, der er fastspændt til det underlag, der definerer vort koordinatsystem. En sådan måling vil også fortælle os om skærmens placering ved kollisionen, og ud fra afstanden mellem spalterne kan vi forudsige den anden partikels position. Men: ved målingen har vi absorberet en helt ukontrollabel impuls i underlaget, hvilket forhindrer os i at bruge impulsbevarelsessætningen på systemet bestående af skærmen og de to partikler. Dette betyder så ikke, at den anden partikels impuls ikke kan måles, men at vi ikke kan definere den uden at foretage en ny i måling; i et grundlag, vores definition, hvile på, er væk. Omvendt vil en måling af den ene partikels impuls nok tillade forudsigelse af den andens impuls, men dette vil medføre en ukontrollabel forskydning af såvel partikel som måleapparat, der fjerner et hvert grundlag for at anstille forudsigelser vedrørende dens position; vi har ikke fastlagt de betingelser, der kunne tillade os overhovedet meningsfuldt at tale om, at den har en position.
For at opsummere kan vi med Bohr konstatere, at disse eksempler på ubestemthedsrelationernes rolle i forbindelse med målinger viser, hvor EPR går galt i byen med deres kriterium for fysisk virkelighed: Umuligheden af i den samme tilstand at give en præcis forudsigelse af målinger på to ikke-kommuterende størrelser repræsenterer ikke en arbitrær udelukkelse af en del af virkeligheden, men afspejler derimod umuligheden af at tilvejebringe omstændigheder, hvorunder begge kan defineres. Det er derfor meningsløst at søge efter en "mere fuldstændig" teori.
4. Realismen og den moderne fysik
EPRs artikel er blot eet af mange lignende angreb på kvanteteorien. De har alle deres udspring i en filosofisk indstilling, der kaldes realisme. Realismen er en doktrin, der (meget groft sagt) går ud på følgende: Verden består af virkelige genstande (real af latin res, ting) med visse egenskaber (attributter). Disse genstande eksisterer uafhængigt af vor sansning af dem, er "objektivt virkelige". Genstandenes attributter opdeles gerne i primære og sekundære: de primære attributter er egenskaber, som genstandene besidder uafhængigt af vore sansninger eller begreber, mens de sekundære er mindre "virkelige" i og med at de ikke kan gives nogen mening uden at referere til en menneskelig iagttager. Et oplagt eksempel på det sidste er en egenskab som "skønhed": en æstetisk vurdering kræver naturligvis en iagttager til at foretage denne vurdering. Men hvilke attributter er nu primære? Forskellige tiders realister har givet forskellige svar:
Anaxagoras mente, at det skulle være størrelse, farve og smag Empedokles anså farve og smag i for antropomorfe, og foretrak størrelse, form og position Den Newtonske fysik er kompatibel med en realisme hvor man anser masse, position og hastighed for primære Men hvad med kvantefysikken?
I følge den sædvanlige fortolkning er kvantemekanikken ikke forenelig med forestillingen om en verden bestående af genstande med objektive egenskaber; de attributter, vi kan udpege, er ikke uafhængige af iagttagelsen, de kan faktisk kun defineres i forbindelse med en bestemt iagttagelsesprocedure. Jagten på primære attributter har visse mindelser om selskabslegen "Jerusalem brænder". Man har ofte hørt den indvending, at selv om vi efter at have målt en partikels impuls har mistet al information om dens position, må den dog stadig være eet eller andet sted, dvs. den må have een eller anden position, som vi blot ikke kender. Men det er netop ikke rigtigt. Position kan kun defineres i forbindelse med eet eller andet referencesystem, en bestemt eksperimentel procedure.
Men hvis (dogmatisk) realisme ikke umiddelbart er foreneligt med kvantefysikken, hvad er så alternativerne?
Heisenberg gør sig til talsmand for en pragmatisk realisme: det vi forstår som objektive egenskaber ved genstandene kan fortsat betragtes som sådan (en klassisk partikel kan fx som sædvanligt siges "virkelig" at have både position og impuls), hvis blot vi husker, at alle sådanne egenskaber er menneskeskabte begreber, som kun kan have begrænset anvendelsesområde. Denne indstilling er i virkeligheden slet ikke realisme i streng forstand, men måske snarere et forslag om en rationel udnyttelse af vort begrebsapparat. Niels Bohr ligger med sit tidligere nævnte komplementaritetsprincip ikke så langt herfra. Her pointeres det, at forskellige klassiske begreber (som position og impuls), som hver for sig er nødvendige for at kunne give en udtømmende beskrivelse af fysiske fænomener, dog ikke kan defineres samtidig. Herved afslører de sig netop også som dele, ikke af en præeksisterende ydre verden, men af et begrebsapparat. Den klassiske fysik er netop en forfinelse af vores sædvanlige (hverdags-)begreber, som netop ikke slår til i den moderne fysik. Komplementaritetsprincippet bygger på den observation, at vi ikke kan undvære de klassiske begreber (da de netop er afledt af vores hverdagssprog), og repræsenterer på en måde en umiddelbar generalisering af disse.
Henry Margeneau foreslår, at man simpelthen afskaffer realismen; det lykkes ham at opbygge en sammenhængende og rationel definition af (fysisk) virkelighed uden overhovedet at referere til en "ydre" verden. Et sådant synspunkt kunne forekomme ekstremt, men det er det i filosofisk forstand i virkeligheden slet ikke - tilfældet er snarere, at et langt mere ekstremt synspunkt (metafysisk realisme) i århundreder - siden Descartes og Locke - har været sat i forbindelse med en helt enestående succesrig videnskab og teknologi (nemlig den klassiske naturvidenskab).
5. Referencer
Jeg har ikke forsøgt at henvise hver eneste gang, jeg bruger en reference. Hovedparten af artiklen er naturligvis skrevet på baggrund af
A. Einstein, B. Podolsky, N. Rosen, Phys Rev 47, 777 (1935)
N. Bohr, Phys Rev 48, 696 (1935)
Begge artikler kan desuden sammen med mange andre spændende artikler om beslægtede emner findes i den i høj grad anbefalelsesværdige
J.A. Wheeler & W.H. Zurek, Quantum Theory and Measurement, Princeton University Press 1983
En grundig behandling af den moderne fysiks erkendelsesteoretiske virkninger findes i bøgerne
Petersen, A., Quantum Physics and the Philosophical Tradition, MIT Press 1968
Margeneau, H., The Nature of Physical Reality, McGraw-Hill 1950
Disse være hermed også anbefalet til alle interesserede.
[ agger, Mon 09 Feb, :21:10:
/artikler/videnskabogfilosofi] -
kommentar(er) -
link
NATURLOVENES RELATIVITET
– af Carsten Agger og Niels K. Petersen
Man hører ofte, at fysikkens opgave er at finde de love, der
bestemmer og forklarer naturens opførsel. Men kan sådanne naturlove
overhovedet eksistere som absolutte og præeksisterende "love" for
naturen, eller er de snarere hjælpemidler for den tanke, der danner de
fysiske teorier? Hvad bygger disse love på, hvad er naturlovenes
natur?
Nature and Nature’s laws lay hid in Night;
God said, Let Newton be! and All was Light.
Som Alexander Popes hyldest til Isaac Newton udtrykker det, er Newton
nok om nogen den, vi kan takke for at have bragt lys over naturens
lovmæssigheder. Med sine Principia Mathematica, sine
matematiske principper for naturfilosofien, formulerede han et sæt
mekaniske love, der f.eks. gjorde det muligt at forudsige himmellegemers
bevægelse. Pope sammenligner denne bedrift med en guddommelig
skaberakt, og Newtons værk må da også betragtes som
højdepunktet af den naturvidenskabelige revolution, der
knæsatte det naturvidenskabelige verdensbillede.
I dette verdensbillede styres universet af universelle
naturlove, der kommer til udtryk i regulariteter, observerbare
regelmæssigheder. De fysiske videnskaber har derfor som et af sine
højeste mål at finde disse love, som sætter dem i stand
til at forstå, forklare og forudsige naturens fænomener og
deres opførsel.
Denne jagt på grundlæggende naturlove fortsætter,
og Newtons love har i mellemtiden vist sig ikke at være
grundlæggende og universelle, men derimod lovmæssigheder, der
under særlige omstændigheder kan udledes af teorier, hvis
antagelser igen bygger på mere fundamentale lovmæssigheder.
Så hvad er egentlig naturlovenes grundlag og natur?
Lovmæssigheder
Regulariteter i naturen er blevet observeret og omsat i kvalitative
eller kvantitative lovmæssigheder langt tilbage i menneskets
historie. Archimedes’ heureka-opdagelse af, at et legeme, der placeres i
væske, vejer lige så meget mindre som massen af den
væskemængde, det fortrænger, er et eksempel. Den
indeholder ikke i sig selv en forklaring på eller teori om, hvad der
sker, men angiver en sammenhæng mellem en årsag og en virkning,
og underforstået: Under nogle særlige (i dette tilfælde
dagligdags) vilkår.
Derimod knytter Aristoteles en teori til sin beskrivelse af en anden
velkendt regularitet, nemlig legemers tendens til at falde, idet han
hævder, at legemer har en tilbøjelighed til at søge mod
deres »naturlige« sted. Imidlertid er såvel styrken som
svagheden ved denne teori eller forklaring, at den er mere filosofisk, end
den er egnet til at forudsige udfaldet af empiriske iagttagelser.
Der har dog i årtusinder været et behov for at
forudsige legemers bevægelse, når det gælder de
regulariteter, der kan iagttages på himlen: Himmellegemernes
bevægelse. Uanset forskellige tiders opfattelse af disse
himmellegemers natur har der været brug for at forudsige
tilbagevendende himmellegemers position. Hvad enten det har været for
at lave kalendere, for at navigere eller af astrologiske årsager, har
det været vigtigt at kende bevægelsen af disse legemer, hvorfor
denne problemstilling og etableringen af underliggende teorier har spillet
en helt central rolle i udviklingen af forskellige former for naturfilosofi
og -videnskab.
Særlig vanskeligt er det at forudsige positionen af det, vi i
dag kender som solsystemets planeter. I antikken og middelalderen kaldtes
de stellae errantes, de omflakkende stjerner, fordi deres baner,
når de observeres fra Jorden, er karakteriseret ved retrograde
bevægelser og sløjfer. Vælger man derfor at anskue
himmellegemerne ud fra en geocentrisk synsvinkel (dvs. med Jorden i centrum
for solsystemet), skal der meget komplekse modeller til, hvor
himmellegemerne f.eks. bevæger sig på cirkler, der
bevæger sig uden på cirkler, såkaldte epicykler.
Sådanne empirisk baserede modeller gør det muligt at lave
meget nøjagtige prognoser for himmellegemers position, og havde der
ikke været andre grunde til at tage det heliocentriske solsystem til
sig, kunne man formodentlig have klaret sig med det geocentriske.
Disse modeller var naturligvis tilknyttet forskellige, hovedsagelig
metafysiske, forklaringer og underlagt antagne forestillinger, men det var
først med såvel matematiseringen af fysikken som betoningen af
den empiriske iagttagelse (eksperimentet) som grundlag for teoridannelsen,
at naturlovsbegrebet begyndte at spille en rolle. Ifølge denne nye
opfattelse af fysikken måtte naturlovene kunne formuleres matematisk,
hvilket muliggjorde nedfældning af lovmæssigheder og love som
dem, Kepler og siden Newton formulerede.
Gravitationsloven og termodynamikkens hovedsætninger
Gravitationsloven er fortsat et af de fornemste eksempler på
en fysisk lovmæssighed og blev endda i lang tid anset for en
universel naturlov. Newton fremsatte den teori, at legemer påvirker
hinanden med kræfter, der virker på afstand. Gravitationsloven
(som også findes behandlet i Faklen nr. 3, s. 34f) angiver en formel
til at beregne størrelse og retning af den kraft, hvormed to legemer
påvirker hinanden, som funktion af deres masser og afstanden imellem
dem. Kraften F er proportional med hver af de to legemers masser
M og m og omvendt proportional med kvadratet på den
indbyrdes afstand r:
hvor G er en proportionalitetskonstant, der kan bestemmes empirisk.
Kraftens retning ligger langs forbindelseslinien mellem de to legemer og
peger ind mod det af de to legemer, der betragtes, hvilket betyder, at
tyngdekraften er tiltrækkende: Det ene legeme graviterer mod det
andet.
Kombineres gravitationsloven nu med Newtons mere generelle love for
kræfter og bevægelse, er det muligt at beregne accelerationen
og hastigheden af en planet, der bevæger sig rundt om Solen. Videre
kan man også konkludere, at genstande tæt ved Jordens overflade
vil falde med praktisk taget konstant acceleration, den lokale
tyngdeacceleration.
Som nævnt er gravitationsloven ikke inden for moderne fysik en
egentlig naturlov, da den mere generelle teori for gravitation er
formuleret i den almene relativitetsteori. Derimod finder vi eksempler
på grundlæggende naturlove inden for varmelæren,
termodynamikken, nemlig de to såkaldte hovedsætninger.
Her betragter man et termodynamisk system, som i praksis kan
være en eksperimentel opstilling, en dampmaskine eller en anden
passende anordning. Systemet afgrænses fra omgivelserne med en
grænseflade, så vi ikke er i tvivl om, hvad der hører
til systemet, og hvad der hører til omgivelserne.
Ifølge termodynamikkens første hovedsætning kan
systemet ikke udføre arbejde, uden at det enten får
tilført eller mister energi. Der gælder med andre ord en
bevarelse af systemets energi, der kan tilføres eller fjernes enten
som mekanisk arbejde eller som varme. Matematisk udtrykkes dette ved, at
ændringen DU i systemets indre
energi U er:
DU = Q + W,
hvor Q er den varmemængde, der tilføres
systemet, og W er det arbejde, der udføres på systemet.
Q og W regnes med fortegn, så negative værdier
angiver, at systemet afgiver varme eller udfører arbejde.
Den totale energi for et termodynamisk system er altså
bevaret. Man kan så måske spørge, hvad energi egentlig
er? For et termodynamisk system kan man tale om to former for energi, den
ene har at gøre med det arbejde, der f.eks. får et hjul til at
dreje rundt, mens den anden har at gøre med den varme, systemet
afgiver eller får tilført. Men hvad knytter egentlig disse to
former for energi sammen?
Fysikeren Richard Feynman har brugt en analogi for at forklare, hvad
energi og energibevarelse er: En dreng har et antal klodser. Hans mor ved,
hvor mange klodser der er, og når drengen har leget med dem, kan hun
tælle klodserne og se, om der er nogle, der er blevet væk.
Mangler der nogle, kan hun så lede efter dem. Tilsvarende kan en af
drengens kammerater komme på besøg og have sine klodser med,
og så finder moderen måske ud af, at drengen har for mange
klodser, og så må hun sørge for, at de overskydende
bliver leveret tilbage til kammeraten. Drengen kan også lege med
klodserne i et badekar, og her kan moderen, jf. Archimedes’ tidligere
omtalte lov, regne sig frem til, hvor mange klodser der ligger i
badekarret, ved at betragte ændringen af vandstanden i
badekarret.
Så moderen ved, at der altid er en størrelse, der er
bevaret, nemlig det samlede antal klodser, uanset hvad drengen ellers har
gjort med dem. Mangler der nogle, er det ikke, fordi antallet af klodser
har forandret sig, men fordi der er klodser, der er havnet et andet sted,
og er der for mange, så er der blevet tilført klodser fra en
kammerats klodssamling. Videre findes der også indirekte metoder (som
ved at betragte vandstanden i badekarret) til at finde frem til antallet af
klodser.
Moderen kan dermed opstille en ligning over alle de måder, hun
har til at finde ud af, hvor mange klodser der er hvor, og mange af dem kan
være indirekte måder, der ikke direkte er relateret til
klodserne, men som er generelle formler.
Feynmans pointe er, at det er ganske samme situation med energi.
Ligesom klodserne kan komme mange forskellige steder hen, har energien
forskellige former, der kan beregnes. Ligesom drengen kan glemme klodser
hos en kammerat, eller kammeraten klodser hos drengen, kan et fysisk system
miste eller blive tilført energi. Og ligesom antallet af klodser er
konstant, er summen af den totale energi konstant. Energi er med andre ord
en bevaret størrelse, en invariant, og termodynamikkens
første hovedsætning fortæller os altså, at der i
sådan et system er to energiformer: Arbejde og varme, og at summen af
disse altid er bevaret.
Den anden hovedsætning er derimod ikke en
bevarelsessætning, men siger, at varme aldrig af sig selv kan
løbe fra et koldt til et varmt sted. Tager man to kopper kaffe, den
ene varm, den anden kold, og bringer dem i berøring med hinanden,
ved vi af erfaring, at den varme afkøles, mens den kolde opvarmes,
indtil begge kopper kaffe har samme lunkne temperatur.
Vi kan opfatte de to oprindelige kopper som en orden, hvor vi har
brugt energi på at koge vand, så vi kan få en kop kogende
varm kaffe, mens denne orden i systemets sluttilstand er forsvundet, og
tilbage er blot en homogen »suppe« af lunken kaffe.
Hovedsætningen formuleres derfor også ofte som, at naturen
stræber mod uorden. Dette kan måske lyde underligt, men
alternativet ville jo være, at vi f.eks. kunne starte med to kopper
lunken kaffe, hvor der så føres varme fra den ene til den
anden, så den koldere kop vedvarende opvarmer den varmere kop. Af
erfaring ved vi, at naturen ikke opfører sig på den
måde, ganske som vi heller ikke forventer, at iltmolekylerne samler
sig i det ene hjørne af det rum, vi befinder os i, men at de i en
eller anden udstrækning er jævnt fordelt over hele rummet.
Når det gælder kaffekoppernes »orden« og
»uorden«, kan vi altså ikke forvente, at processen kan
føres tilbage fra den lunkne sluttilstand til den ordnede
starttilstand. Processen er med andre ord irreversibel. Betragter vi
derimod gravitationsloven, er der intet i gravitationslovene og Newtons
øvrige love, der forbyder planeterne at følge den samme bane
i den modsatte retning. Legemernes bevægelse er med andre ord et i
princippet reversibelt fænomen.
De to hovedsætninger supplerer hinanden. Den første
hovedsætning gælder for såvel reversible som irreversible
processer, fordi energien jo vil være bevaret, uanset hvordan den
fordeler sig mellem de to kaffekopper, så alene ud fra den
første hovedsætning kunne energien godt flyde fra den koldere
kop til den varmere. Den anden hovedsætning gælder også
for såvel reversible som for irreversible processer, men den udstyrer
os med et værktøj til at finde ud af, om en proces er
reversibel eller irreversibel. Rent teknisk udtrykkes hovedsætningens
stræben efter »uorden« ved at sige, at en bestemt
størrelse, der kaldes entropien, aldrig kan aftage. For
reversible processer er entropien konstant, mens den vokser for
irreversible. Når den varme kop afkøles, og den kolde
opvarmes, øges entropien med andre ord, og sluttilstandens entropi
er altså større end starttilstandens. Men da entropien aldrig
kan aftage, er det dermed ikke muligt at vende tilbage til starttilstandens
lavere entropi. Tilsammen afgrænser de to hovedsætninger
altså de mulige termodynamiske processer.
Karakteristisk nok er den første hovedsætning
altså en bevarelsessætning, for sætninger eller love, der
siger, at en eller anden fysisk størrelse, som f.eks. energien, er
bevaret, er fundamentale inden for fysikken, hvilket igen svarer til
analogien med klodserne. Fysikeren finder det måske nok vanskeligt at
forklare, hvad energi egentlig er, men han kan forklare, hvordan
energien er en nyttig størrelse at operere med, fordi den er
bevaret. Man kan derfor lidt groft påstå, at sådan en
bevarelsessætning er en slags trossætning, fordi der ikke
findes et empirisk bevis for den. På den anden side vil læseren
nok være enig i, at moderen i klodsanalogien i princippet altid vil
kunne finde en forklaring på, hvad der er blevet af det totale antal
klodser, om ikke andet så fordi vi af erfaring ved, at klodser ikke
bare forsvinder ud i den blå luft. På samme måde
forventer fysikeren, at en grundig undersøgelse af, hvad der sker
med et fysisk system, vil kunne gøre rede for, hvad der sker med den
totale energi i systemet. Energien forsvinder ikke og opstår ikke ud
af intet.
Igen er det ikke noget, der kan bevises, men læseren ville
formodentlig blive ikke så lidt overrasket, hvis et koldt legeme
afgav varme til et varmt, og derfor er der næppe heller nogen fysiker
eller ingeniør, der f.eks. vil bruge tid på folk, der
hævder at have opfundet en evighedsmaskine. Sådan en maskine
må nødvendigvis bryde med termodynamikkens
hovedsætninger ved f.eks. at levere arbejde til omgivelserne uden at
modtage en tilsvarende mængde varme, og det vil læseren
sandsynligvis også finde ret utænkeligt. Så skønt
energibevarelse og termodynamikkens hovedsætninger ikke kan bevises,
svarer de ganske nøje til al empirisk erfaring.
Bevarelsessætninger og symmetri
Energibevarelse betyder mere generelt, at summen af den totale
energi i et isoleret system forbliver den samme til ethvert tidspunkt.
Inden for kvantefysikken er det endda sådan, at det er energien, der
styrer et fysisk systems udvikling i tid, og den er dermed afgørende
for udfaldet af et eksperiment eller i hvert fald for sandsynligheden for
et givet udfald. Eftersom man ved en eventuel reproduktion af et
eksperiment på et isoleret system må forvente, at udfaldet er
uafhængigt af, hvilket tidspunkt eksperimentet udføres
på, må systemets totale energi derfor være den samme til
enhver tid. Energibevarelsen har altså på et mere fundamentalt
niveau at gøre med, at fysikkens love er, eller forventes at
være, de samme til ethvert tidspunkt.
At man går ud fra, at det principielt er ligegyldigt,
hvornår man udfører et eksperiment, er baseret såvel
på erfaringen som på den antagelse, at alle tidspunkter er
»lige gode« i fysisk forstand – at tiden ikke har nogen
»egenskaber«, der påvirker de fysiske love – hvilket igen
bygger på den intuitive forestilling, at de fysiske love ikke
varierer fra tid til anden. Skulle det nemlig vise sig, at der var en
sådan diskontinuitet i fænomeners udvikling, er det mest
nærliggende at søge efter en underliggende mekanisme, der
forklarer diskontinuiteten. Det er ganske som med moderen, der ikke kan
finde en klods. Hun forventer heller ikke, at klodsen pludselig er
ophørt med at eksistere, men derimod blot, at hun endnu ikke har
ledt alle de steder, hvor klodsen kan være havnet.
Energibevarelsen er altså knyttet til en grundlæggende
forestilling om, at fysikkens love er uafhængige af, hvornår et
eksperiment udføres. Et eksperiment, der udføres til et
tidspunkt t1, vil altså kunne forklares ud fra de samme
fysiske love, som hvis det blev udført til et andet tidspunkt
t2. De fysiske love er altså de samme under en
tidsforskydning, og en sådan tidsforskydning ændrer ikke
på den totale energi: Energien er invariant.
Når de fysiske love er de samme under en tidsforskydning,
kalder man det en symmetri, og der er altså til denne symmetri
knyttet en invariant størrelse: Energien. Symmetri er naturligvis
velkendt i geometrisk forstand som et fascinerende, æstetisk og
nyttigt fænomen, men inden for fysik og matematik har det en
særlig definition og praktisk rolle. Ligesom invarians har symmetri
at gøre med en eller anden form for »lighed«. En symmetrisk
genstand kan jo f.eks. være en, hvor vi ved at dreje genstanden ikke
kan skelne mellem genstanden før og efter drejningen. Drejes
eksempelvis et kvadrat 90 grader, kan vi ikke skelne kvadratet før
drejningen fra kvadratet efter drejningen, netop fordi kvadratet er
symmetrisk.
90 graders drejningen er et eksempel på en matematisk
operation, og når man i mere generel forstand taler om symmetri,
mener man, at der findes en matematisk operation, som man kan påvirke
en genstand med, så det ikke er muligt at skelne mellem genstanden
før og efter operationen. Operationen skal naturligvis ikke
være triviel eller omfatte alt i universet, for hvis man drejer alt,
har man jo ikke drejet genstanden i forhold til noget.
Inden for fysikken er det ikke nødvendigvis en geometrisk
lighed, der opnås ved en symmetrilighed, men derimod fysikkens love,
der gælder, uanset den benyttede symmetrioperation. Vi kan f.eks.
forestille os, at vi befinder os i Århus og her gennemfører en
serie fysiske eksperimenter. Vi udfører derefter en operation
på denne starttilstand ved at flytte laboratoriet – det kan jo
være et mobilt laboratorium – til Odense, hvor vi så
gennemfører den samme serie fysiske eksperimenter. Resultaterne af
eksperimenterne vil ret sikkert ikke være helt de samme, da en lang
række lokale og temporale forhold kan påvirke eksperimenterne,
men man vil i overensstemmelse med erfaringen forvente, at vi kan forklare
begge sæt resultater ud fra de samme fysiske lovmæssigheder.
Eksempelvis gælder gravitationsloven overalt på Jordens
overflade, når man f.eks. undersøger faldende genstande, selv
om tyngdeaccelerationen varierer fra sted til sted.
Den operation, hvormed vi forskyder positionen af det fysiske
system (i dette tilfælde laboratoriet), er altså en symmetri.
En sådan forskydning kaldes en translation, og der
gælder altså translationssymmetri. Denne symmetri er knyttet
til en grundlæggende forestilling om universet og de fysiske love,
idet den fortæller os, at der ikke findes en position i rummet, der
er noget særligt frem for andre positioner; man siger, at rummet er
homogent.
Tilsvarende kan vi i stedet for at flytte det mobile laboratorium
vælge at dreje det om en akse, så det eksperimentelle udstyr
peger i en anden retning. Nu vil det næppe overraske læseren,
at der ved denne operation, der naturligt nok kaldes en rotation,
heller ikke kan skelnes mellem de fysiske love, der beskriver resultatet af
eksperimenterne, hvorfor det altså gælder, at de fysiske love
er rotationssymmetriske. Ganske analogt til, at der ikke findes en
særlig position i rummet, findes der heller ikke nogen særlig
retning i rummet; fysikkens love gælder, uanset hvilken retning vi
kigger i. Denne egenskab ved rummet betegnes isotropi.
Som nævnt er der ikke tale om absolutte naturlove, der kan
anses for bevist, men derimod om principper, som stemmer overordentlig godt
med såvel vore dagligdags som eksperimentelle erfaringer og
forventninger til, hvordan naturen opfører sig. Symmetrierne knyttet
til tidslige eller rumlige forskydninger og til rotationer kan måske
ligefrem forekomme oplagte, men det er ingen garanti for, at der ikke
findes fænomener i naturen, der bryder med disse symmetrier, ligesom
det heller ikke betyder, at alle symmetrier er oplagte. Tværtimod
beskæftiger en meget stor del af fysikken sig med fænomener,
der befinder sig så langt væk fra hverdagens, at det er
vanskeligt at anskueliggøre mange symmetrier i et ikke-teknisk
sprog.
Er det således relativt oplagt, at der kan gælde
translationssymmetri, er det næppe i samme grad oplagt, at der
også er en symmetri under den operation, hvor vi ikke blot flytter
laboratoriets position, men hvor hele laboratoriet bevæger sig med en
jævn, retlinet hastighed i forhold til den oprindelige position.
Denne symmetri blev opdaget af Galilei, hvorfor operationen kaldes
galileitransformationen. Galilei lod således en af personerne
i dialogen Dialogo sopra i due massimi sistemi del mondo (1623)
forestille sig, at man indretter et simpelt laboratorium på et skib.
F.eks. kan man hænge en flaske med vand op, så den drypper. Man
observerer så, hvordan dråberne falder, når skibet ligger
stille, og hvordan de falder, når det sejler roligt afsted med
jævn hastighed. Galilei konkluderer, at man ikke kan kende forskel
på dråbernes fald. De følger præcis den samme
bane, og tilsvarende med Galileis øvrige eksperimenter. Der
gælder med andre ord symmetri under galileitransformationen.
Det gør der til gengæld ikke, hvis skibet begynder at
accelerere, dvs. hvis vi til galileitransformationen tilføjer en
acceleration. Det er velkendt fra f.eks. en bustur, at man kan sidde
nogenlunde roligt, når bussen kører afsted med jævn
hastighed, men i det øjeblik bussen bremser, sætter farten op
eller drejer, så kan der straks ske noget dramatisk, der gør
det nødvendigt at holde fast. Det er med andre ord muligt at skelne
mellem et fysisk system (bussen), der er i hvile eller bevæger sig
med jævn hastighed, og det samme fysiske system, der accelererer.
De nævnte symmetrier har været kendt længe, men
interessen for dem skyldes et vigtigt resultat, som matematikeren Emmy
Noether opdagede for knap hundrede år siden. Hun viste, at der til
enhver symmetrioperation findes en bevaret størrelse. Inden for
fysikken betyder det, at hver eneste gang, man kan finde en symmetri, vil
der være en bevarelsessætning, og det har igennem det tyvende
århundrede vist sig at være en overordentlig praktisk
viden.
Vi har allerede betragtet et eksempel: Til den symmetrioperation,
hvor et tidspunkt forskydes til et andet, hører energibevarelse.
Tilsvarende findes der for andre symmetrier andre fysiske
størrelser, der er bevaret. Til en rumlig forskydning, en
translation, hører bevarelse af en størrelse, der kaldes
impuls og er givet ved et legemes masse ganget med dets hastighed
(jf. også artiklen »Iagttagelsesafhængighed og teoribygning«
i Faklen nr. 3), og til rotationssymmetri en størrelse kaldet
impulsmoment. Drejer det sig om en partikel, der roterer om en akse
i afstanden r fra aksen, og har partiklen impulsen p = mv,
hvor m er partiklens masse og v dens hastighed, er
impulsmomentet J = rp = rmv.
Dette lyder måske meget teknisk, men bevarelsen af
impulsmomentet har mange konsekvenser i hverdagen. Når f.eks. en
skøjtedanser laver en pirouette, kan hun ændre på sin
omdrejningshastighed ved at variere kropsstillingen. Strækkes
hænderne ud, vil hun rotere langsommere, end når hun holder
hænderne ind til kroppen. Det skyldes netop, at impulsmomentet (hvis
vi forestiller os, at isen er uendelig glat, så der ikke er nogen
gnidning mellem skøjterne og isen) er bevaret, hvorfor afstanden fra
hænderne til rotationsaksen, der går op gennem
skøjtedanserens krop, er omvendt proportional med hastigheden.
Spejlingssymmetri
Forbindelsen mellem symmetrier og bevarelsessætninger betyder,
at vi kan knytte alle de af fysikkens love, der har karakter af
bevarelsessætninger, til grundlæggende egenskaber ved rummet og
naturen. Men der foreligger altid den mulighed, at nye opdagelser, nye
eksperimenter, kan gøre det nødvendigt at revidere vores
opfattelse af disse grundlæggende egenskaber. Der er utallige
fortilfælde, hvor man har været ganske sikker på, at
verden var indrettet på en bestemt måde, mens den
videnskabelige forskning uundgåeligt har ledt frem til at forkaste
den slags tilsyneladende indlysende og naturlige principper, såsom at
man før Kepler mente, at himmellegemernes bevægelse skulle
beskrives ved cirkelbaner, fordi cirklen blev regnet for perfekt.
Derfor kan også fundamentale forestillinger, herunder
symmetrier, stå for fald. Et eksempel er spejlingssymmetri, der
betyder, at vi med de samme fysiske love kan beskrive såvel et fysisk
eksperiment som en version af eksperimentet, der er et perfekt spejlbillede
af den eksperimentelle opstilling. Spejlingssymmetrien svarer til, at vi
ikke kan angive et eller andet fysisk eksperiment, der gør det
muligt at skelne mellem højre og venstre, mellem op og ned.
Indtil 1950erne blev spejlingssymmetri anset for en
gennemprøvet og selvfølgelig egenskab ved naturen, og ingen
ventede vel, at man skulle finde fysiske fænomener, der rent faktisk
gør det muligt at skelne mellem højre og venstre. Ikke desto
mindre var det netop det, der skete, da man udforskede de såkaldte
svage vekselvirkninger. Ved disse fysiske processer udsendes der
typisk såkaldte neutrinoer, der er masseløse partikler.
Neutrinoerne reagerer uhyre sjældent med det stof, de passerer, og
det er derfor, man taler om svage vekselvirkninger. Faktisk passerer der
hele tiden et astronomisk antal af dem igennem hver enkelt af os, men
sandsynligheden for, at bare en af dem reagerer med et af kroppens atomer,
er uhyre lille, hvilket for eksperimentalfysikerne betyder, at det
kræver megen tålmodighed at observere bare en enkelt
neutrino.
Et af de første eksperimenter, der viste, at
spejlingssymmetrien ikke gælder processer, der er styret af svage
vekselvirkninger, drejede sig om at studere den elektron, der udsendes fra
en radioaktiv atomkerne, der henfalder via svage vekselvirkninger. Den
ustabile kerne må i eksperimentet have et såkaldt spin.
Man kan f.eks. tænke på en snurretop for at få en
fornemmelse af, hvad et spin er. Snurrer toppen mod uret, er spinnet
ifølge konventionen rettet i én retning (nemlig »op«),
mens det er rettet i den anden retning (»ned«), hvis toppen snurrer
med uret. Eksperimentet har nu til formål at bestemme sandsynligheden
for, at elektronen bliver sendt ud i samme retning som kernens spin.
Hvordan vil denne idealiserede forsøgsopstilling tage sig ud
i et spejl? En snurrende tops spejlbillede vil rotere i den modsatte
retning af selve toppen. Spejlbilledet vil derfor have det modsatte spin af
toppen. Udsendes elektronen ved henfaldet nu i samme retning som toppens
spin, vil den i spejlet blive udsendt modsatrettet spejlbilledets spin.
Hvis der derfor skal gælde spejlingssymmetri, så vi ikke kender
forskel på op og ned, må sandsynligheden for, at elektronen
bliver udsendt i samme retning som kernens spin være lige så
stor som, at den bliver udsendt modsat rettet kernens spin.
Men eksperimenterne viste, at langt de fleste elektroner, der
udsendes fra sådanne kerner, blev udsendt i den ene retning, og
få i den anden, hvorfor sandsynligheden ikke er lige stor. Man kan
derfor definere »højre« som f.eks. den retning, hvor flest
elektroner bliver udsendt i forhold til kernernes spin, og på den
måde skelne mellem højre og venstre.
Det er dog fortsat kun inden for den del af naturen, der styres af
de svage vekselvirkninger, hvor spejlingssymmetrien bryder sammen. For alle
andre processer gælder symmetrien, men medmindre vi hårdnakket
mener – som nogle gør – at der findes en underliggende teori,
der er spejlingssymmetrisk, og som forklarer, hvorfor spejlingssymmetrien
tilsyneladende ikke gælder de svage vekselvirkninger, må vi ud
fra de empiriske resultater acceptere, at der rent faktisk findes
måder at skelne mellem højre og venstre, mellem op og ned!
Geometri og rummets natur
Naturlovene er altså via bevarelsessætninger knyttet til
de egenskaber, vi erfaringsmæssigt vil tillægge verden,
herunder rummet. Vores opfattelse og formulering af naturlovene må
derfor nødvendigvis være afhængig af, hvilken geometri
vi benytter til at beskrive rummet. I årtusinder har det været
den geometri, som Euklid aksiomatiserede i sine Elementer ca. 300
f.v.t., og som følgelig kaldes den euklidiske geometri. Det
er denne geometri, der forekommer mest naturlig, og som man lærer om
i skolen. Geometrien, hvor summen af vinklerne i en trekant er 180 grader,
hvor Pythagoras’ sætning om, at summen af kvadraterne på en
retvinklet trekants kateter er lig hypotenusens kvadrat, gælder, og
hvor parallelle linier aldrig skærer hinanden. Og det er den
geometri, som filosoffen Kant anså for den eneste mulige.
Imidlertid arbejdede matematikere som Gauss, Bolyai og Lobachevsky i
det 19. århundrede på nye geometrier, hvor vinkelsummen i en
trekant kan være større eller mindre end 180 grader, og hvor
parallelle linier alligevel kan skære hinanden. I første
omgang var dette måske mest akademiske resultater affødt af et
par årtusinders spekulationer over især Euklids postulat om, at
parallelle linier aldrig skærer hinanden, men man behøver dog
ikke tænke på noget mere eksotisk end jordoverfladens geometri
for at finde et eksempel på en ikke-euklidisk geometri.
Denne geometri, der kaldes sfærisk geometri, fordi den
beskæftiger sig med geometrien på overfladen af en kugle (en
sfære – i praksis kan man til mange formål antage, at Jorden
er formet som en perfekt kugle), adskiller sig netop på
væsentlige områder fra den euklidiske geometri. I
modsætning til plangeometriens uendelige, flade plan, hvor parallelle
linier kan fortsætte i det uendelige uden nogen sinde at
mødes, har overfladen af en kugle en endelig udstrækning, og
den længst mulige »lige« linie er en såkaldt storcirkel,
der går hele vejen rundt om kuglen og har centrum i kuglens midte. En
af konsekvenserne af denne sfæriske geometri er, at vinkelsummen i en
trekant, hvor tre storcirkler skærer hinanden, er større end
180 grader. Det hænger sammen med krumningen af kuglens
overflade, hvorfor man ved at betragte geometrien på en overflade med
en anden krumning f.eks. kan finde, at trekantens vinkelsum altid er mindre
end 180 grader.
Det er klart, at den sfæriske geometri har mange praktiske
anvendelser, f.eks. inden for skibs- og flyfarten, men det er også
velkendt, at Einstein i sin almene relativitetsteori forkastede den
euklidiske geometri til fordel for et firedimensionalt ikke-euklidisk
kontinuum, hvor tiden indgår som en dimension. Det betyder, at mange
af de egenskaber, vi er tilbøjelige til at anse for oplagte ved
rummet, ikke nødvendigvis gælder. Eller i hvert fald, at de
kun gælder under ganske lokale forhold.
I dagligdagen, hvor de færreste bevæger sig over
strækninger, der er så store, at det er nødvendigt at
tage højde for Jordens krumning, kan man nemlig klare sig med den
euklidiske geometri, og det er da også sådan inden for
fysikken, at man lokalt for et eksperimentelt system kan lade, som om
universet er fladt, at det er euklidisk. Men der er her blot tale om en
praktisk approksimation, fordi enhver fysiker ved, at rum-tiden ikke er
euklidisk.
Betragter man til gengæld helt generelt en ikke-euklidisk
firedimensional rum-tid, kan man ikke forudsætte, at symmetrierne for
tidslige eller rumlige forskydninger stadig holder. Er der således
ingen symmetri under en tidslig forskydning, er det ikke muligt at
opretholde en energibevarelse, hvilket ikke betyder, at energibevarelsen
bryder sammen, men at energibegrebet ikke giver nogen mening i det
pågældende system. Ligesom den klassiske fysiks forestilling om
et univers af partikler, der til et givet tidspunkt må befinde sig
på en bestemt position, bryder sammen i kvantefysikken, hvor det i
almindelighed ikke giver mening at tale om, at en partikel overhovedet kan
tillægges en bestemt position, bryder energibevarelsen sammen i den
almene relativitetsteori; ikke i den forstand, at energien påviseligt
ikke er bevaret – det er ganske enkelt ikke muligt at
definere begrebet »energi«.
I den almene relativitetsteori er det fordelingen af legemer med
masse, der krummer rum-tiden, eller for at sige det på en anden
måde: Tyngdefeltet er ækvivalent med rum-tidens krumning. Det
er derfor tyngdefeltet i det konkrete system, der er afgørende for,
om man i et lokalt afgrænset system kan finde symmetrier og dermed
bevarelsessætninger. Det kan man i specielle tilfælde, hvoraf
det i særdeleshed må gælde for systemer, hvor man
fuldstændig kan se bort fra tyngdefeltet, eller det i det mindste er
meget svagt. Her bliver rum-tiden nemlig henholdsvis fuldstændig
eller praktisk taget euklidisk.
Den generalisering, der ligger i den almene relativitetsteori, er
altså ikke som sådan et opgør med den universelle
energibevarelse, men derimod en udvidelse af fysikkens teoribygning, der
dermed kommer til at omfatte et bredere sæt af fysiske
fænomener, hvis opførsel ikke kan forklares eller forudsiges
ved hjælp af ellers værdsatte symmetrier og
bevarelsessætninger, men derimod ved relativitetsteoriens mere
generelle ligninger og lovmæssigheder.
Newtons gravitationslov, der som tidligere omtalt er et af de
fornemste eksempler på en lovmæssighed i naturen, er
således også et specialtilfælde af den mere generelle
beskrivelse i den almene relativitetsteori. Den gælder i den
såkaldte Newtonske grænse, hvor man vælger at anskue
fysiske fænomener under forhold, der minder om dem, Newton antog om
rum og tid, og for fænomener som dem, Newton beskæftigede sig
med, eksempelvis planetbevægelser. I dette specialtilfælde kan
man sagtens benytte Newtons kraftbegreb i stedet for rum-tidens krumning
til at forklare og forudsige legemers bevægelse.
Man kan altså sige, at Einstein henviste Newtons opdagelse til
at være et specialtilfælde, og det er karakteristisk for
fysikkens teoridannelse, at tidligere triumfer senere bliver særligt
interessante specialtilfælde i mere generelle teorier. Skønt
Newtons præstation hermed synes at stå noget tilbage for
Alexander Popes hyldest, var kronen på værket måske
også snarere end at afdække naturlovene at udstyre fysikerne
med en metode til at forklare og forudsige fysiske fænomeners
opførsel.
Naturlovene er således først og fremmest
generalisationer af observerede regulariteter, som er underlagt de
begrænsninger og udtrykkes i det sprog, der er særegent for de
teorier om verdens indretning, som de udspringer af. De har i mange
tilfælde form af en bevarelsessætning, som igen via en symmetri
kan hænge sammen med fundamentale egenskaber, fysikerne
tillægger naturen, såsom at udfaldet af et eksperiment ikke
afhænger af, om det udføres til et tidspunkt eller et andet.
Det kan også være en rent erfaringsmæssig regel som
termodynamikkens anden hovedsætning, der udelukker visse processer
fra at være fysisk mulige. Skønt sådanne fundamentale
egenskaber ofte synes at bekræfte relativt intuitive opfattelser af,
hvordan naturen må være skruet sammen, kan fysikeren aldrig
vide, om udfaldet af et eksperiment gør det nødvendigt at
forkaste selv meget hævdvundne forestillinger om visse princippers og
lovmæssigheders almengyldighed. Det gælder for
spejlingssymmetriens sammenbrud for svage vekselvirkninger og for
relativitetsteoriens opgør med tilvante forestillinger om tiden og
rummet.
Lovmæssighederne kan måske nok opretholdes inden for
visse områder eller i specialtilfælde, som når man kan
forlade sig på Newtons gravitationslov i dagligdagen, men i
almindelighed udvides teorierne til stadighed med de nye fænomener,
der opdages. Denne proces fortsætter, og skønt det er
nærliggende at opfatte processen som en stadig tilnærmelse til
et sæt universelle naturlove, der beskriver, hvordan verden »i
virkeligheden« opfører sig, er dette en illusion; vi kan nemlig
aldrig vide, hvor tæt vi kommer på sådanne a priori love,
og det kan til enhver tid gå med den aktuelle opfattelse af, hvordan
naturen er indrettet, som det er gået med spejlingssymmetrien og med
opfattelsen af, at rummet skal beskrives med euklidisk geometri. Der findes
altså ingen »naturlove« i den forstand, der ligger i ordets
betydning: Et sæt universelle spilleregler for verdens
opførsel.
Det er i denne forstand, at naturlovene er relative. Selv om de
på den ene side er et praktisk og uundværligt
værktøj til at opnå fysikkens mere grundlæggende
mål, at forklare og forudsige fysiske systemers opførsel, kan
selv de mest veletablerede naturlove ikke påberåbe sig
almengyldighed. Inden for denne begrænsning forbliver de et
konceptuelt værktøj, hvis gyldighed under bestemte,
veldefinerede betingelser kan anses for så veldokumenteret, at den
ikke kan betvivles. Så længe der opdages nye fænomener i
naturen, og så længe der er et behov for at forstå og
beskrive disse fænomener, vil naturlovene derfor udvikle sig – og
dermed hele vores opfattelse af, hvordan verden er indrettet.
Oprindelig bragt i Faklen nr. 19, 2001
[ agger, Sun 27 Apr, :09:07:
/artikler/videnskabogfilosofi] -
kommentar(er) -
link
IAGTTAGELSESAFHÆNGIGHED OG TEORIBYGNING
- af Carsten K. Agger og Niels K. Petersen
Kvantefysikken har vendt op og ned på den traditionelle opfattelse
af forholdet iagttagelsen og det iagttagede imellem. Her følger i
store træk en gennemgang af naturvidenskabens vej til disse
resultater og en analyse og tilbagevisning af nogle af de
væsentligste indvendinger mod den såkaldte
københavnerskoles fortolkning af implikationerne for vor
virkelighedsopfattelse.
Fysik og naturfilosofi
Fysikken blev i moderne forstand grundlagt i det 16.
og 17. århundrede, hvor Galilei og Newton indførte den
kvantitative iagttagelse, målingen, som den grundpille,
hvorpå den af fysikken indhentede viden må bygges.
Den fremstod dog først som en enkelt, samlet
disciplin i slutningen af forrige århundrede; indtil da var det, vi i
dag forstår ved fysik, indeholdt i forskellige grene af
naturfilosofien som mekanik, akustik, optik, varmelære og
elektricitetslære.
Forrige århundredes syntese af forskellige
discipliner til én videnskab hang blandt andet sammen med opdagelsen
af, at forskellige fænomener som varme, lyd og lys, der oprindelig
var blevet betragtet som fundamentalt forskellige, kunne behandles som
manifestationer af nogle få, mere grundlæggende mekanismer. For
eksempel opdagede Faraday i 1831, at et magnetisk felt, der ændrer
sig med tiden, kan inducere en elektrisk strøm i et kredsløb,
hvormed han viste, at elektricitet og magnetisme, der tidligere havde
været betragtet som adskilte fænomener, er to sider af samme
sag.
I slutningen af det 19. århundrede havde alle de
oprindelige discipliner således vist sig at kunne reduceres til to,
mekanikken og elektromagnetismen.
Fysikken beskæftiger sig i princippet med verden
og naturen som sådan; ordet er netop afledt af det græske
physis, der betyder natur. Mere præcist søger fysikken
at udforske sammenhænge mellem verdens bestanddele og
vekselvirkningerne imellem dem. Således handler fysikken først
og fremmest om den ikke-levende natur, om legemers og partiklers
bevægelse i tid og rum og de kræfter, der virker mellem dem, og
dermed også om de mest grundlæggende spørgsmål om
stoffets og tidens og rummets natur og struktur.
I denne forstand er fysikken naturligvis en direkte
fortsættelse af den antikke græske naturfilosofi, af
Aristoteles' teorier om substans, kræfter og bevægelse og af
Demokrits atomteori.
Man hører ofte, at den moderne naturvidenskab
adskiller sig fra den antikke naturfilosofi ved udelukkende at grunde sig
på erfaringen, hvor den antikke var rent spekulativ, og hvor man
formodedes at kunne tænke, ræsonnere sig frem til en
erkendelse af, hvordan verden var indrettet.
Dette er imidlertid ikke helt rigtigt. Mange af de
græske filosoffers teorier var netop udledt som abstraktioner eller
generaliseringer af almindelige erfaringer. Når Aristoteles (ganske
vist fejlagtigt) fastholdt, at ting falder, fordi de har en tendens til at
falde proportionalt med deres vægt, og at tunge ting derfor vil falde
hurtigere end lette, er det jo netop udledt af erfaringen: en sten falder
vitterlig hurtigere til jorden end et stykke brød af samme
størrelse (på grund af luftmodstanden, som Aristoteles
altså forsømte at tage højde for).
Den reelle forskel mellem det antikke og det moderne
synspunkt ligger i, at naturfilosoffernes overvejelser var kvalitative i
stedet for kvantitative. Efter at Galilei indførte matematikken som
fysikkens egentlige sprog, spørger fysikeren ikke længere om,
hvad der sker, og hvordan det sker, men i stedet om, hvor meget og hvor
hurtigt: de fysiske teorier bliver rent kvantitative. En forudsigelse i en
fysisk teori bliver derfor en påstand om, at en konkret måling
vil give et bestemt, kvantitativt resultat.
Dette betyder ikke, at man ikke interesserer sig for
fænomenernes kvalitative egenskaber; oplysninger om disse fremkommer
blot altid på baggrund af en kvantitativ teori.
I den klassiske fysik vil en redegørelse for et
givet systems tilstand altså bestå i en angivelse af
værdierne til forskellige tider af de målelige
størrelser, der karakteriserer de forskellige dele af systemet.
Newtons gravitationslov
Det simplest tænkelige eksempel på et
sådant system er en enkelt partikel, der er under påvirkning af
en (her ikke nærmere specificeret) kraft. En redegørelse for
dens tilstand på et givet tidspunkt består i 6 tal (x, y, z,
vx, vy, vz), der angiver partiklens position og
hastighed.
Et andet eksempel er vand, der strømmer i et
rør, hvor systemets tilstand kan angives ved en specifikation af
vandets hastighed og retning i ethvert punkt. En fysisk teori vil nu kunne
redegøre for et sådant systems opførsel, hvis man ud
fra den kan opstille en matematisk model, der, givet en starttilstand,
nogle dynamiske love eller bevægelsesligninger og nogle
antagelser om systemets vekselvirkninger gør det muligt at beregne
systemets tilstand til ethvert tidspunkt. Alle kvalitative
spørgsmål om systemet må nu udledes af den herved
fremkomne rent matematiske models forudsigelser.
Et klassisk eksempel på en sådan teori er
Newtons gravitationslov, som var en af den klassiske mekaniks tidligste
succeser.
Efter flere års studier af Tycho Brahes
observationer af stjernehimlen lykkedes det Kepler at opstille 3 love for
planeternes bevægelse omkring Solen:
1) Planeterne bevæger sig i elliptiske baner
med Solen i det ene brændpunkt.
2) Arealet af den del af ellipsen, der
udspændes af Solen og planetens position til to forskellige
tidspunkter med for eksempel en dags eller en måneds mellemrum, er
konstant.
3) Middelafstanden A fra Solen opløftet til
tredje potens divideret med kvadratet på omløbstiden T er
konstant for alle planeter, dvs. Aü /Tý = konstant.
I mekanikken er den fundamentale bevægelsesligning
Newtons anden lov, der udsiger, at den totale kraft, der virker på en
partikel, er identisk med partiklens masse ganget med accelerationen i dens
bevægelse. I et system af flere partikler skyldes disse kræfter
partiklernes vekselvirkning, der afhænger af deres indbyrdes
position.
Bevægelsesligningen for en planets bevægelse
omkring Solen vil da (udtrykt i ord) udsige, at planetens acceleration til
enhver tid vil være givet ved en (endnu ukendt) funktion af dens
position i forhold til Solen.
Af Keplers første og anden lov lader det sig
relativt nemt - omend med en anelse matematisk besvær - vise, at
denne kraft for det første kun kan afhænge af planetens
afstand r til Solen og for det andet må være omvendt
proportional med kvadratet på denne afstand. Antages denne kraft -
gravitationen - ydermere at være en egenskab, der gælder for
alle massive legemer, kan vi antage, at kraften er proportional med begge
legemers masse. Alt i alt giver dette os Newtons gravitationslov:
F = GMm/rý
hvor F betegner kraften mellem de to legemer,
M og m de to masser, og konstanten G er den såkaldte
gravitationskonstant. Denne lov, som altså kan udledes af Keplers og
Newtons love kombineret med et par grundlæggende antagelser, kan med
stor nøjagtighed forklare planeternes bevægelse omkring Solen,
herunder deres hastighed på ethvert punkt i banen og deres
omløbstider.
Man vil imidlertid som regel ikke stille sig tilfreds
med en fysisk teori, der kun forklarer de eksperimentelle data eller (som i
dette tilfælde) empirisk bestemte lovmæssigheder, den skulle
forklare. Derudover må den kunne tilbyde en model, der kan bruges til
at udfinde sammenhænge, som man ikke tidligere var klar over.
Lad os se på, hvorledes gravitationsloven
honorerer dette krav. For det første er det relativt enkelt at bruge
den til at udlede Keplers tredje lov. For det andet forudsiger den, at
genstande nær Jordens overflade alle vil falde med den samme
acceleration, hvilket først blev påvist af Galilei; denne
acceleration lader sig nu let beregne ud fra gravitationskonstanten og
Jordens masse og radius. Teorien forbinder himmellegemernes bevægelse
med den tyngdekraft, genstande på Jorden er underlagt, og
understreger altså det krav, der må stilles til en fysisk
teori: den skal forklare de kendte eksperimentelle resultater og
gå et skridt videre ved at afdække nye sammenhænge eller
forudsige resultatet af hidtil ukendte eksperimenter - og disse
forudsigelser eller sammenhænge må derefter verificeres
eksperimentelt. Først da kan teorien siges at være
bekræftet, og først da repræsenterer den en ny indsigt.
Klassisk fysik - objektivitet og materialisme?
Den klassiske fysiks verdensbillede bygger, som det
vil forstås, på forestillingerne om rum og tid: en beskrivelse
af et system er en redegørelse for tilstanden ethvert sted i rummet
på ethvert tidspunkt. Den verden, den beskriver, antages dermed at
eksistere i sig selv, helt uafhængigt af nogen iagttager eller
iagttagelse: en objektiv virkelighed.
Betyder dette nu, at den klassiske fysik forsøger
at opdage, hvordan verden ¯virkelig® er? Eller sagt på en anden
måde: er denne den klassiske fysiks ¯objektivitet® udtryk for
en epistemologisk realisme, og er det berettiget at tage den klassiske
fysiks succes til indtægt for en materialistisk filosofi (der antager
eksistensen af en objektiv, reelt eksisterende verden, der er helt
uafhængig af vor iagttagelse af den)?
Det er her vigtigt at være opmærksom
på, at den klassiske fysiks teorier og forklaringer som regel
repræsenterer skrupelløse forenklinger, der ikke
forsøger at indfange, hvordan verden virkelig er, men i stedet
forsøger at give et anvendeligt billede af situationen. Man ser for
eksempel ofte bort fra luftmodstanden i diverse faldproblemer, fra Solens
indvirkning på Månens banebevægelse om Jorden, eller man
ser bort fra væskers og metallers atomare struktur og opfatter dem
som kontinuerte medier, osv. Og pointen er, at hvis man tog højde
for alle disse ting, ville man blot opnå en mere kompliceret model,
der måske var i bedre overensstemmelse med det eksperimentelt
observerede, men som ikke derfor umiddelbart ville kunne siges at have
større eller mindre lighed med nogen verden, som den kunne formodes
at eksistere i sig selv.
Objektiviteten er således blot en spilleregel i
den klassiske fysiks modelbygning, og det viser sig da også, at mens
denne således i teorien synes at forudsætte en epistemologisk
realisme, gør den det ikke i praksis. Dette kan blandt andet ses af,
at man ofte tillader sig at gøre forenklende antagelser, som det
ville være fuldstændig absurd at tage alvorligt som
påstande om verden i sig selv, men som i realiteten er redskaber,
hvis værdi ligger i den indsigt, de kan give i observerbare
fænomener.
Som helt banale eksempler kan nævnes, at man ved
beregning af planeternes banebevægelser ofte ser helt bort fra
virkningen af de andre planeter, men regner, som om Solens
tiltrækning alene var ansvarlig for planetens opførsel, at man
ved behandling af atomstrukturen i faste stoffer kan lade som om, kun
nærmeste naboer påvirker hinanden, at plader er uendeligt
store, eller at universet kun består af de partikler, der er
relevante for det problem, man interesserer sig for.
Mere elaborate eksempler er Drudes teori for metaller
(fra slutningen af forrige århundrede), hvor metallets elektroner
antoges at opføre sig som en gas af partikler, der bevægede
sig frit rundt i hele metallet uden at vekselvirke med hinanden, mens
atomkernerne blot postuleredes at være ubevægelige, eller Bohrs
atommodel, hvor elektronerne kun kan bevæge sig i ganske bestemte
baner om kernen: da der (ifølge postulatet) ikke findes noget mellem
disse baner, kan elektronen kun afgive eller optage energi i diskontinuerte
spring.
I Einsteins teori for krystalsvingninger i faste stoffer
(1907) antog han, at alle atomerne i et krystal altid svingede med samme
frekvens. Her som i Drude-modellen er det oplagt, at, hvordan disse
systemer end måtte være indrettet, så er teoriens
antagelser i al fald ikke rigtige. Alligevel gav disse modeller (bl.a. ved
ret præcise forudsigelser af de observerede egenskaber for visse
metaller) en aldeles uundværlig indsigt i de faste stoffers struktur.
Og dette viser igen tydeligt, at selv om de klassisk-fysiske teorier som
spilleregel udtaler sig om en objektivt eksisterende verden,
indebærer de en fri modeldannelse, hvor modellerne kun
bedømmes ud fra, hvor godt de kan forklare de observerede
fænomener.
Einsteins relativitet og Heisenbergs ubestemthedsrelationer
Den klassiske fysik forsøger altså at
finde frem til de love, der bestemmer stoffets fordeling og bevægelse
til forskellige tidspunkter. Tid og rum antages at være entydigt
definerede, således at for eksempel et bestemt tidsrum eller et
bestemt linjestykke altid vil være lige langt for alle
observatører. I den specielle relativitetsteori, som Einstein
udledte i 1905, antages lysets hastighed imidlertid at være den samme
for alle iagttagere, der bevæger sig uden acceleration.
Denne antagelse bryder så afgørende med
vore sædvanlige forestillinger, at man for at forstå dens
implikationer for begreberne tid og rum må analysere disses betydning
ud fra deres definition, det vil sige: man må angive, hvordan de i
princippet kan måles (se f.eks. Feynman [1]). En konsekvens af denne
analyse er den berømte Lorentz-kontraktion, at genstande, der
bevæger sig med stor hastighed i forhold til en iagttager, fra denne
iagttagers synspunkt trykkes sammen i bevægelsens retning.
Her giver det således kun mening at tale om
afstanden mellem to punkter eller om, at to begivenheder er samtidige, hvis
man specificerer, fra hvilket system de tænkes iagttaget. Tid og rum
ophører dermed med at være givne størrelser og bliver
til en del af fysikkens genstandsområde. Men ikke nok med det: hvor
den ¯gamle® klassiske fysik beskrev en objektiv verden, hvor tid og
rum er givne, absolutte størrelser, indeholder relativitetsteorien
altså en eksplicit reference til en iagttager: med i
beskrivelsen af selve systemet hører angivelsen af, hvorfra det
tænkes iagttaget. Systemet antages dog stadig at eksistere
uafhængigt af selve iagttagelsen.
Dette er ikke tilfældet i kvantemekanikken, som er
den fysiske teori, der anvendes til at beskrive mikroskopiske systemer. Den
kvantemekaniske teori blev udviklet i kølvandet på en lang
række tilsyneladende paradoksale eksperimentelle resultater. En
vigtig konsekvens af denne teori er Heisenbergs
ubestemthedsrelationer, ifølge hvilke det ikke er muligt at
måle visse par af fysiske størrelser (i kvantemekanikken ofte
betegnet observable) med vilkårlig nøjagtighed. Denne
ubestemthed har at gøre med måleapparaturets påvirkning
af det system, man observerer, og medfører, at de iagttagede
fænomener ikke blot afhænger af, hvilken type system man
vælger at observere, men også af, hvilken specifik
eksperimentel opstilling, der vælges.
For at illustrere, hvad der menes med, at det iagttagede
fænomen afhænger af den valgte eksperimentelle opstilling, vil
vi se på det vel nok simplest tænkelige eksempel: en enkelt
partikel og dens bevægelse.
I fysikken beskrives bevægelse oftest ikke ved at
angive partiklens hastighed, men derimod dens impuls, som er
defineret som produktet af hastigheden og partiklens masse. Impulsen kaldes
også undertiden bevægelsesmængde, og dens betydning
ligger hovedsagelig i den såkaldte impulsbevarelsessætning, der
er én af mekanikkens fundamentale love: den samlede impuls af et
system før og efter en given reaktion eller
vekselvirkning vil altid være den samme - der er aldrig observeret
noget brud på denne regel. Heisenbergs ubestemthedsrelation siger for
et sådant system, at produktet af usikkerheden D
x på positionen og D
p på impulsen, mindst er halvdelen af en konstant kaldet Plancks
konstant (sædvanligvis betegnet med h) divideret med 2p
:
D
xD
p ³
h/2p
Plancks konstant er meget lille, og derfor vil vi
normalt ikke observere nogen ¯kvanteubestemthed® i vores
makroskopiske dagligdag. Vi observerer dog, at relationen begrænser
den nøjagtighed, hvormed de to størrelser kan kendes samtidig
- vi kan for så vidt måle partiklens position med næsten
uendelig præcision, men må så samtidig give
fuldstændig afkald på at udtale os om partiklens
bevægelse. Sådanne par af fysiske størrelser, der ikke
kan defineres samtidig, kaldes ofte komplementære.
Ubestemthed og vekselvirkning med måleapparatet
I kvantemekanikkens matematiske formalisme beskrives
et sådant system af dets bølgefunktion, hvis fysiske
betydning ikke er umiddelbart visualiserbar; den kan betragtes som en slags
sandsynlighedstæthed, idet kvadratet på den i et givet punkt i
rummet repræsenterer sandsynligheden for ved en måling at finde
partiklen på dette sted. Hvor partiklen er, eller hvad resultatet af
en sådan måling vil blive, udtaler teorien sig ikke om; den
tillader kun at beregne sandsynligheden for, at en måling af
partiklens position vil give et bestemt resultat. Før målingen
er foretaget, giver det overhovedet ikke mening at sige, at partiklen har
en position.
Dette kan indses selv uden at komme ind på den
matematiske formalisme, ved at analysere ubestemthedsrelationernes
betydning for vores muligheder for at måle to komplementære
størrelser som position og impuls.
Hvis vi forestiller os, at vores partikel skydes igennem
en enkelt spalte i en skærm, kan vi straks se, at usikkerheden
på partiklens position, umiddelbart efter den har passeret spalten,
dels må være bestemt af spaltens bredde, dels af selve
skærmens position. Vi antager, at partiklens impuls før
kollisionen er kendt, og at spalten er meget tynd, det vil sige så
tilpas tynd, at en angivelse af skærmens position umiddelbart efter
kollisionen sammen med en opmåling af skærmen vil give os en
præcis bestemmelse af partiklens position. Kan vi omvendt måle
skærmens impuls efter kollisionen, kan vi ud fra den ovenfor
nævnte impulsbevarelsessætning give en præcis bestemmelse
af partiklens impuls.
Men hvad kan en måling af den ene af disse
størrelser nu betyde for vores muligheder for at udtale os om den
anden?
Hvis vi ønsker at bestemme partiklens position,
kan vi spænde skærmen fast til underlaget i en bestemt
højde og lade partiklen passere igennem; til gengæld vil
vekselvirkningen med skærmen føre til, at der absorberes en
ukontrollabel mængde impuls i underlaget, hvorfra partiklen
observeres. Dette introducerer naturligvis en ubestemthed i partiklens
impuls efter kollisionen, så det er helt umuligt for os at forudsige
partiklens impuls f.eks. ved hjælp af
impulsbevarelsessætningen.
Hvis vi derimod ønsker at bestemme partiklens
impuls, kan vi i stedet forestille os skærmen ophængt i en
fjeder eller lignende, så den kan bevæge sig frit. Hvis vi nu
måler dens impuls før kollisionen, kan vi gentage
målingen bagefter; herefter kan vi ved hjælp af
impulsbevarelsessætningen forudsige partiklens impuls efter
kollisionen (idet systemets totale impuls skal være den samme
før og efter). Denne fremgangsmåde kræver imidlertid en
nøjagtig bestemmelse af skærmens impuls; som følge
heraf introduceres der altså (igen ifølge
ubestemthedsrelationen) en ubestemthed i skærmens position, der
gør det umuligt at bruge skærmen til at bestemme partiklens
position.
I begge tilfælde ser vi, at bestemmelsen af den
ene størrelse udelukker, at man samtidig kan bestemme den anden -
skulle vi således efter at have bestemt partiklens position
også ønske at kende dens impuls, ville denne måling
kræve endnu en vekselvirkning med måleapparatet, der igen ville
ødelægge vores bestemmelse af positionen.
Har vi således foretaget en præcis
bestemmelse af en partikels position, kan vi altså ikke meningsfuldt
hævde, at den bevæger sig med en bestemt hastighed eller
impuls; det er i princippet umuligt at definere denne bortset fra som
potentiel: en måling af den vil give en bestemt værdi (med en
sandsynlighed, der kan beregnes ud fra bølgefunktionen).
Einstein, Podolsky og Rosens indvendinger - og Bohrs svar
Einstein, Podolsky og Rosen (EPR) fandt i deres
berømte artikel fra 1935 [2], at denne situation, hvor de fysiske
størrelser ikke kan tillægges nogen bestemt værdi, hvis
ikke de måles, ikke afspejlede noget fundamentalt ved verden, men
simpelt hen skyldtes en ufuldstændighed i kvantemekanikken, idet der
ved fuldstændighed forstås, at teorien giver en
udtømmende beskrivelse af de betragtede fænomener. Hvordan nu
det?
Lad os forestille os, at vi har hængt
skærmen op, så den kan bevæge sig frit, målt dens
impuls og ladet partiklen passere. Denne situation brugte vi ovenfor til at
bestemme partiklens impuls, men vi har faktisk flere muligheder: en
måling af partiklens position vil naturligvis tillade os at bestemme
skærmens position (idet partiklens position jo bestemmes af spalten i
skærmen), og så videre.
Ifølge kvantemekanikken er det i denne situation
umuligt at give en eksakt forudsigelse af værdien af impulsen eller
positionen for nogen af de to komponenter - disse værdier defineres
først i det øjeblik, vi faktisk beslutter os for at
måle en af dem. Men måler vi så den ene komponents
impuls, har vi dermed fastlagt den andens, og måler vi den enes
position, kan vi igen forudsige den andens. Vi har kort sagt at gøre
med, hvad man kalder en entangled state.
EPR argumenterede nu, at vi jo ved for eksempel at
måle partiklens impuls derved éntydigt kan forudsige
skærmens - vælger vi omvendt at måle dens position, har
vi samtidig bestemt skærmens position. Men denne måling
på det ene system kan jo nu - efter kollisionen er overstået,
og de to komponenter er holdt op med at vekselvirke - umuligt påvirke
det andet. Derfor, argumenterede EPR, må impuls og position for begge
komponenter være veldefinerede på forhånd, og
kvantemekanikkens beskrivelse, hvor disse først defineres ved
målingen, er altså ufuldstændig.
Dette argument blev dog imødegået af Bohr
[3], der fremhævede, at målingen af for eksempel partiklens
position uundgåeligt - alene som en konsekvens af
ubestemthedsrelationen - vil medføre en absorption af impuls i
underlaget, der forhindrer os i at bruge impulsbevarelsessætningen,
og dermed simpelt hen fjerne ethvert meningsfuldt grundlag for at
definere skærmens impuls. Der er altså ikke tale om
nogen mekanisk påvirkning; der er derimod tale om, at målingen
påvirker de betingelser, der tillader os overhovedet at definere de
pågældende fysiske størrelser.
Man kunne også bruge skærmen fra som en del
af en større opstilling, det såkaldte
dobbeltspalteeksperiment. Partiklen kan efter at have passeret spalten i
skærmen gå gennem den ene eller den anden spalte i den
mellemste skærm, hvorefter den vil blive registreret af en
fotografisk plade på bagvæggen.
Vi lader igen skærmen være ophængt,
så den kan bevæge sig frit, lader partiklen passere gennem
anordningen og registrerer dens position på den fotografiske plade.
Hvad skete der? Hvilken spalte passerede partiklen
igennem?
Dette spørgsmål kan vi besvare ved at
måle den bevægelige skærms impuls, efter partiklen har
passeret den - herudfra kan vi beregne partiklens retning umiddelbart efter
kollisionen og dermed, hvilken spalte den gik igennem.
Hvad nu, hvis vi i stedet holdt skærmen
fastspændt til underlaget? Hermed fjerner vi som nævnt ethvert
grundlag for at udtale os om partiklens impuls og dermed retning, efter den
har passeret spalten - hermed giver det simpelt hen ikke mening at sige, at
den skulle være passeret gennem den ene eller den anden spalte. I
stedet vil dens bølgefunktion udbrede sig gennem begge spalter, og
udføres eksperimentet mange gange, vil der på bagvæggen
opbygges et interferensmønster.
Vælger vi at fastlægge partiklens
begyndelsesposition, vil den altså i dette eksperiment opføre
sig som et bølgefænomen og bevæger sig i en forstand
igennem begge spalter og ingen af dem; fastlægger vi i stedet
begyndelsesimpulsen, opfører den sig som en partikel og
bevæger sig pænt igennem den ene eller den anden spalte. Men i
tilfældet med den bevægelige skærm kan vi jo stadig,
efter eksperimentet er udført og partiklen registreret, selv
vælge, om vi vil måle partiklens position (ved at spænde
skærmen fast til underlaget og måle dens position) eller impuls
(ved at måle skærmens impuls); det vil sige, at vi, efter det
hele er overstået, selv kan bestemme, om partiklen passerede gennem
den ene eller begge spalter.
Hvis man som EPR vil insistere på, at
fænomenet skal kunne beskrives, som det er i sig selv,
uafhængigt af iagttagelsen, må man altså acceptere, at
virkningen - om partiklen bevæger sig gennem én af spalterne
eller evt. dem begge, om vi har at gøre med et partikel- eller
bølgefænomen - kommer før årsagen, nemlig
fastlæggelsen af en bestemt begyndelsesimpuls eller -position. Dette
repræsenterer naturligvis ikke nogen kausal virkning tilbage i tiden,
men skyldes vores endelige fastlæggelse af det grundlag, hvorpå
vi kan bygge en beskrivelse eller forudsigelse af partiklens adfærd.
Det er netop en accentuering af, at det studerede fænomen ikke kan
siges at eksistere uafhængigt af målingen, men kun er defineret
ved en specifikation af hele den eksperimentelle opstilling.
Niels Bohr og dagligsproget
Denne opfattelse af kvantemekanikken opstod i
kredsen omkring Niels Bohr og blev siden af Werner Heisenberg betegnet
¯københavnerskolen®. Den betegnes også
¯standardfortolkningen®, fordi det er den måde at
beskæftige sig med kvantemekanikken, der siden har været den
fremherskende. Dens tilhængere opfatter den også gerne som den
eneste mulige.
Bohrs ¯fortolkning® er tæt knyttet til hele
hans opfattelse af forholdet mellem fysik og det begrebsapparat, man
benytter til at dyrke fysik med. Den reproducerbare eksperimentelle
situation er fysikkens fundament, og til den fordres muligheden af entydigt
at kunne kommunikere eksperimentets opbygning, udførelse og
resultat. Dette nødvendigvis entydige deskriptive sprog, som Bohr
kaldte ¯dagligsprog®, udgør en del af det, vi almindeligvis
vil kalde dagligsprog, og finder i Bohrs tankegang sin præcisering i
matematikken og den klassiske fysik: ¯Med ordet 'eksperiment' henviser
vi til en situation, hvor vi kan fortælle andre, hvad vi har gjort,
og hvad vi har lært, samt at forsøgsanordningen og
måleresultaterne derfor må beskrives i det sædvanlige
sprog med passende anvendelse af den klassiske fysiks terminologi.®
(Bohr [4]).
Dagligsprogets deskriptive egenskab betyder, at der
må impliceres et skel mellem et beskrivende subjekt og et beskrevet
objekt, altså en dualisme. Entydigheden implicerer, at
subjekter er ombyttelige. Det er altså muligt for forskellige
subjekter at beskrive det samme objekt inden for dagligsprogets rammer.
Hertil kommer, at dagligsprogets objekter må kunne lokaliseres i rum
og tid, og at der kan gives et deterministisk årsag-virkningsforhold
mellem begivenheder.
Denne logik og dualisme gælder for den deskriptive
del af alle sprog: ¯Ved objektivitet vil vi forstå en beskrivelse
ved hjælp af et sprog, der er fælles for alle (ganske bortset
fra sprogforskellighederne mellem nationer), og på hvilket mennesker
kan meddele sig til hverandre på det område, hvorom talen er.®
(Bohr [5]). Al fysik må altså nødvendigvis forstås
via dagligsprog og dets forfining, klassisk fysik, der netop er
karakteriseret ved at honorere dagligsprogets egenskaber.
Kvantefysikkens fænomener kan ligeledes kun
tillægges mening inden for denne begrebsramme, da vi fortsat må
kunne beskrive dem entydigt. Det er endda sådan, at observationen af
disse fænomener kun kan foregå i situationer, der hører
til den klassiske fysiks domæne, fordi det forsøgsapparatur,
der i sidste ende fører til en måling, kan beskrives ud fra
den klassiske fysik alene.
Vi er under alle omstændigheder nødt til at
forstå et hvilket som helst af fysikkens fænomener inden for
den begrebsramme, der udgøres af klassisk fysik og
¯dagligsprog®, hvis vi overhovedet vil tale fysik. Et hvilket som
helst fænomen kan dermed i sidste ende kun tillægges en mening
inden for disse begrebers rammer.
Vil man derimod tale om fænomener, der ikke er
defineret inden for begrebsapparatets ramme, må vi
nødvendigvis benytte begreberne forkert, hvorfor beskrivelsen bliver
paradoksal. Et eksempel på en sådan paradoksal sprogbrug er
det, når man taler om, at et kvantefænomen både er en
partikel og en bølge samtidig med, at det er ingen af delene. En
sådan sprogbrug er meningsløs, hvis man vil kommunikere
entydigt, og det er derfor principielt umuligt at tale om fysiske
¯fænomener®, der ikke eksisterer inden for dagligsprogets
begrebsramme: ¯I denne forbindelse taler man somme tider om
'forstyrrelse af fænomenerne ved iagttagelse' eller 'skabelse af
atomare objekters fysiske attributter ved målinger'. Sådanne
udtryk er imidlertid vildledende, idet ord som fænomener og
iagttagelse såvel som attributter og målinger her er benyttet
på en med fælles sprog og praktisk definition uforenelig
måde. Med henblik på objektiv beskrivelse er det mere
hensigtsmæssigt kun at bruge ordet fænomen til at henvise til
iagttagelser vundne under omstændigheder, hvis beskrivelse
indbefatter en redegørelse for hele forsøgsanordningen.®
(Bohr [6]). Begrebsrammen udgøres i kvantefysikkens tilfælde
af den eksperimentelle opstilling og dens resultater.
At tale om, hvorvidt fotonen bevæger sig igennem
den ene eller den anden spalte i et dobbeltspalteforsøg, er
meningsløst fra et fysisk synspunkt, medmindre forsøget netop
er indrettet således, at det er muligt at detektere, hvilken spalte
fotonen bevæger sig igennem. Men så opstår der, som vi
så i diskussionen af EPRs tankeeksperiment, heller intet
interferensmønster. At tale om det ligger uden for fysikkens
grænser, det er metafysik.
Vi ¯hænger i sproget®
Problemstillingen ses også tydeligt i nyere
eksperimenter, hvor man i analogi med dobbeltspalteeksperimentet kan
spørge, ¯hvilken vej® fotonen tog. I disse eksperimenter er
det faktisk muligt at modificere eksperimentet således, at man kan
besvare spørgsmålet uden at få problemer med Heisenbergs
ubestemthedsrelation. Til gengæld får man så også
et resultat, der stemmer overens med ¯partikelbilledet®, idet der
ikke opstår noget interferensmønster.
Et relativt simpelt eksempel på et sådant
eksperiment blev udført af Zajonc et al. [7]. Lys fra en laser
splittes op i to i en beam splitter. Fotonen kan så sendes i
en af to såkaldte ikke-lineære krystaller, hvor fotonen
¯omdannes® til et fotonpar, hvoraf hver foton har den halve energi af
den oprindelige. Disse to fotoner kaldes traditionelt på engelsk
signal og idler.
Forsøgsopstillingen indrettes nu således,
at en detektor opfanger signal-fotoner og en anden idler-fotoner. Disse
arrangeres således, at idler-fotonerne fra de to krystaller
¯følger den samme bane® til idler-detektoren, mens
signal-fotonerne ¯følger forskellige baner®. Opstillingen
arrangeres nu således, at fotonerne når frem til detektorerne
på samme tid uafhængigt af, hvilken krystal de blev dannet i.
Da en sammenligning af detektionerne af signal-fotoner
og idler-fotoner ikke kan skelne fotoner fra den ene krystal fra den anden,
bliver resultatet af et stort antal forsøg et
interferensmønster i signaldetektoren. Holdes nu en hånd ind
foran den første krystal, så idler-fotonen forhindres i at
nå frem til detektoren, er det muligt at skelne mellem signal-fotoner
fra de to krystaller. Detekteres der nemlig en signal-foton, men ingen
samtidig idler-foton, kommer signal-fotonen fra den første krystal,
mens en simultan detektion af signal- og idler-foton betyder, at
fotonparret kommer fra den anden krystal. Der dannes derfor ikke et
interferensmønster i signal-detektoren, eksperimentet er et
¯partikel®-eksperiment. En simpel modifikation af
forsøgsopstillingen kan altså ændre eksperimentet fra et
¯bølge®- til et ¯partikel®-eksperiment.
Mere sofistikerede eksperimenter af denne art, hvor en
lille ændring af den eksperimentelle opstilling kan give oplysning
om, ¯hvilken vej® fotonen bevægede sig, er også blevet
udført. Et sådant eksperiment kaldes af og til en quantum
marker, mens en modifikation, der fjerner denne information, kaldes en
quantum eraser. Et særlig vellykket eksempel blev
udført af Herzog et al. [8], der også udførte
eksperimentet med et forsinket valg af, om man vil udføre et quantum
marker- eller eraser-eksperiment.
Det forsinkede valg træffes, efter eksperimentet
er indledt. Dets rationale er at se, om der er nogen eksperimentel evidens
for en realistisk fortolkning af, hvad der ¯sker i eksperimentet®. De
eksperimentelle resultater er fuldt ud i overensstemmelse med
kvantemekanikkens bølge-partikel-komplementaritet, og dette resultat
kan kun forklares realistisk ved at bruge en paradoksal sprogbrug, hvor det
forsinkede valg betyder, at virkningen kommer før årsagen.
Dette er et alvorligt opgør med fysikkens
tradition for at ¯visualisere® de fysiske fænomener og teorier.
Det er således ikke længere muligt at danne sig et billede af
fotonen uden for målesituationen, hvilket dog ikke afholder fysikeren
fra at tegne små bølger eller partikler, når et
forsøg skal diskuteres. Trangen til at benytte en ¯visualisering®
eller ¯intuitiv® model hidrører fra, at vi jo netop
¯hænger i sproget®, som Bohr udtrykte det [9], og selv en
paradoksal sprogbrug kan være en første hjælp til at
komme ind på livet af en eksperimentel situation, der ellers kun kan
bearbejdes formelt.
Til gengæld sikrer Bohrs ¯dagligsprog®, at
det er meningsfuldt for en fysiker at tale om, at et klassisk fysisk objekt
som en planet var på et sted til en tid, selv om ingen observerede
den på det tidspunkt. Bohrs understregning af sprogets rolle er
altså en præcisering af, hvad vi overhovedet mener, når
det gælder fysik: ¯It is wrong to think that the task of physics
is to find out how nature is. Physics concerns what we can say about
nature® (Bohr [10]). Fysik drejer sig altså om at
kommunikere om naturen. Dette er dog ikke en realisme i ontologisk
forstand, for erkendelssituationen ¯what we can say about nature®
implicerer ¯nature® som et begreb i dagligsproget, og ikke
¯nature® i nogen ontologisk realistisk forstand.
Bohr kunne derfor heller ikke forlige sig med ethvert
forsøg på at tale om noget, der befinder sig uden for
dagligsproget. Valget mellem idealisme og realisme var i Bohrs øjne
et meningsløst spørgsmål: ¯Materialism and
spiritualism, which are only defined by concepts taken from each other, are
two aspects of the same thing® (Bohr [11]). Mennesket er ikke i stand
til at ¯træde uden for® begrebsapparatet og kommunikere med
andre mennesker om verden. Iagttageren - i den forstand vi overhovedet
definerer det begreb - er en del af verden: vi er samtidig skuespillere og
tilskuere i tilværelsens store drama, som han udtrykte det (Bohr
[12]).
Kritikken af københavnerskolen
Bohr understregede altså begrebsapparatets
rolle og beskæftigede sig dermed med, hvorledes begreberne skulle
bruges på en entydig måde. Denne indstilling kan betegnes som
en pragmatisme, der ikke beskæftiger sig med begreber i anden
forstand end den, der er givet af begrebsrammen. Det er derfor
meningsløst at tillægge den dualisme, der er en uadskillelig
del af begrebsapparatet, anden mening end den rent begrebslige. At
hævde, at begreberne i en eller anden forstand har absolut betydning
uden for denne begrebsramme, er derfor en absurditet.
For fænomener i klassisk fysisk forstand er det
meningsfuldt at tale om deres eksistens i tid og rum til ethvert tidspunkt,
men definitionen af disse fænomener er fortsat uløseligt
knyttet til en observationel situation. At tale om fundamentalt
uobserverbare fænomener er at øve vold mod begrebsapparatet.
Kvantemekanikkens overvældende succes teoretisk og
teknologisk giver os ikke nogen grund til at mistænke den for at
være fejlagtig, så potentielle modstandere må enten
påvise, at dens beskrivelse er ufuldstændig, eller at det er
muligt at beskrive kvantefænomenerne på anden vis i en
ikke-paradoksal sprogbrug.
Fuldstændigheden kan ikke bevises, men vi har
ingen fysisk grund til at formode, at kvantemekanikken ikke skulle
være fuldstændig. Der kan derimod nok være filosofiske og
metafysiske årsager til at betvivle den, som også var
baggrunden for EPRs kritik. Dens ophavsmænd forfægtede nemlig
det standpunkt, der kaldes lokal realisme, idet lokalitet er den
fysiske egenskab, at det er muligt at udføre en måling
på et af to ikke-vekselvirkende systemer uden at påvirke det
andet. Denne antagelse blev netop benyttet i gennemgangen af EPRs
argumentation, da det blev antaget, at de to komponenter ikke kunne
vekselvirke efter kollisionen.
Einstein var notorisk for ikke at acceptere de
erkendelsesmæssige konsekvenser af kvantemekanikken, således
som Bohr og kredsen om ham opfattede dem. Siden har mange forsøgt at
gøre op med københavnerskolens ¯ortodoksi®, men har i
bedste fald blot formuleret alternative ¯fortolkninger®, hvis
berettigelse fortsat er tvivlsom.
Karakteristisk for disse forsøg er, at man vil
påføre enten kvantefænomenerne eller selve formalismen
en ontologisk realitet. Således har man søgt at indføre
realistiske modeller ved at postulere, at kvantefænomenerne kan
karakteriseres ved hidtil ukendte parametre, såkaldte skjulte
variable, der skulle tillade en ikke-paradoksal beskrivelse af
kvantefænomenerne uafhængigt af forsøgsopstillingen og
målingen. Mange af disse forsøg er formelt matematisk blevet
tilbagevist, og enkelte ligefrem empirisk.
I klassisk fysik angiver formalismen gerne f.eks.
tidsudviklingen af en fysisk målelig variabel, hvorfor formalismen i
sig selv kan henføres til noget fysisk. For en realistisk indstillet
fysiker er det derfor nærliggende at spørge om, hvad
bølgefunktionen ¯egentlig® er. Dette er klart et metafysisk
spørgsmål, hvis besvarelse strengt taget er irrelevant for
fysikken. Bølgefunktionen kan jo per definition ikke observeres; det
eneste, der kan observeres, er begivenheder, hvis statistiske fordelinger
er givet ved bølgefunktionens kvadrat.
Ved selve målingen bliver et af de mulige udfald
af eksperimentet til en måling. Denne ¯udvælgelse® af et
resultat til en måling kaldes ofte bølgefunktionens
kollaps, og det kan derfor også være nærliggende
at spørge til en ¯fysisk® mekanisme, der ligger bag kollapset.
Dette er endnu et meningsløst spørgsmål set fra
¯standardfortolkningens® synspunkt, for kollapset angiver jo blot, at
en måling har fundet sted, hvorved det overhovedet er blevet
meningsfuldt at tale om et fysisk fænomen.
En særlig form for fortolkning af
bølgefunktionen findes i den såkaldte
mange-verdensfortolkning, der oprindelig blev fremsat af Hugh
Everett i 1957 [13]. Ifølge denne sker der aldrig noget kollaps af
bølgefunktionen, når der foretages en måling, men
universet deler sig i parallelle universer, hvor hvert muligt udfald af
observationen er aktuelt i de respektive paralleluniverser. Er der
således to udfald af et eksperiment, vil observatøren i det
ene univers opnå det ene udfald, mens observatøren i det andet
vil opnå det andet udfald. Det ¯reelle® fænomen bliver da
bølgefunktionen, der er en superposition af de forskellige mulige
udfald, mens observatøren er et fænomen underordnet udfaldene.
Denne opfattelse muliggør derfor opstillingen af en
bølgefunktion for hele universet, idet den omfatter både
observatøren og det observerede.
Mange-verdensteorien vender således op og ned
på begreberne og postulerer den paradoksale og tilsyneladende
ubeviselige eksistens af paralleluniverser, der netop på grund af, at
der rent faktisk foreligger en konkret måling i hvert separat
univers, er uafhængige, hvorfor det ikke er fysisk muligt inden for
kvantemekanikkens rammer at detektere andre paralleluniverser end det,
hvori man selv befinder sig og foretager målinger.
Erkendelsesteoretisk er mange-verdensteorien derfor i højeste grad
metafysisk, men den har en vis tiltrækningskraft på fysikere
inden for visse felter.
Hardys teorem
John Stewart Bell påviste i 1964 en matematisk
relation, Bells ulighed, der i princippet muliggjorde en simpel test
af EPRs lokale realisme versus kvantemekanikken [14]. Flere andre
tilsvarende resultater er siden blevet fundet, bl.a. i det overbevisende
GHZ-tankeeksperiment [15]. Her vil vi illustrere problemstillingen med et
beslægtet og ret simpelt resultat, der betegnes Hardys teorem
efter Lucien Hardy. Der er tale om et tankeeksperiment, der
anskueliggør teoremets indhold uden nærmere at specificere de
betragtede fysiske størrelser (Mermin [16]). Når der
således tales om ¯partikler®, menes der blot et eller andet
kvantefysisk objekt, og de ¯spørgsmål®, der omtales, er
simpelt hen målinger af relevante fysiske størrelser. Men alle
tankeeksperimentets resultater er beregnet ud fra kvantemekanikkens
formalisme.
Forsøgsopstillingen består af en kilde, der
udsender to ¯partikler®, og to detektorer, der er anbragt langt
væk fra kilden. Hver detektor gør det muligt at få
svaret ja eller nej på et af to spørgsmål: den ene
detektors spørgsmål benævnes A og B, den andens M og N.
Hvilke af spørgsmålene, der skal besvares, bestemmer
eksperimentatoren, og opstillingen er indrettet således, at det er
muligt at vente med at vælge svarene, indtil partiklerne er sendt
afsted. Det er også muligt at indrette opstillingen således, at
spørgsmålet på den ene detektor først
vælges, når der er svaret på det spørgsmål,
der er valgt på den anden.
Lad nu A/M = ja/nej betegne, at svaret på
spørgsmål A er ja, og svaret på M er nej, når
spørgsmålene A og M er valgt, og tilsvarende for de andre
mulige spørgsmål og svar. Det viser sig nu
¯eksperimentelt®, at der gælder følgende:
1. B/N = ja/ja forekommer af og til.
2. B/M = ja/ja forekommer aldrig.
3. A/N = ja/ja forekommer aldrig.
4. A/M = nej/nej forekommer aldrig.
Disse resultater betyder, at det ikke er muligt at
forudsige svaret på det andet spørgsmål ved et passende
valg af det første spørgsmål. Dette ses eksempelvis ved
at betragte valget A/M. Hvis M = nej, betyder 4, at A = ja; hvis derimod M
= ja, kan svaret på A være både ja og nej. Vælges i
stedet for A/N, vil A = nej, når N = ja (iflg. 3.), men svaret
på A kan være både ja og nej, når N = nej.
Nu indrettes forsøgsgangen således, at
valget af spørgsmål er tilfældigt, og valget finder
først sted, når partiklerne har forladt kilden.
Helt grundlæggende antages det, at der ikke
forekommer nogen vekselvirkninger mellem partiklerne, når de har
forladt kilden, og heller ikke mellem detektorer og partikler. En
koordinering af, hvilke svar de to partikler vil give på de mulige
spørgsmål, kan altså kun forekomme i kilden og er
fuldstændigt uafhængig af valget af spørgsmål, der
jo først finder sted, når partiklerne har forladt kilden.
Hvert af de valgte spørgsmål besvares kun ved informationer
fra netop den ene partikel, der når den pågældende
detektor, og altså ikke ved informationer fra den anden partikel.
Lad os nu analysere de eksperimentelle fakta: fra 1 ved
vi, at ved valget B/N vil der af og til forekomme svarene ja/ja.
Ifølge vore antagelser er partiklen, der giver svar på
spørgsmål B, en partikel, der altid vil give svaret ja
på spørgsmål B, og tilsvarende vil den anden partikel
altid give svaret ja på spørgsmål N. Hvis valget nu var
blevet B/M, måtte svaret på spørgsmål B
altså være ja, og ifølge 2 må svaret på M
være nej, altså B/M = nej/nej. Hvis omvendt valget nu var
blevet A/N, skulle partiklen, der giver svar på
spørgsmål N, fortsat give svaret ja, og ifølge 3
må så svaret på A være nej, altså A/N =
nej/ja. Endelig kunne valget være blevet A/M, og ifølge vore
antagelser og det ovenstående må partiklerne på disse
spørgsmål give svarene nej/nej, men dette er i modstrid med 4.
Hardys teorem siger altså, at den
ovenstående antagelse om lokalitet er i modstrid med
kvantemekanikken, hvorfor kvantemekanikken i denne forstand er ikke-lokal.
En eksperimentel test af Bells ulighed blev rent faktisk
udført med de eksperimenter, Alain Aspect udførte
først i firserne [17], hvis resultater som andre fysiske
eksperimenter kan diskuteres, men det er rimeligt at sige, at der er en
bred opfattelse af, at EPRs lokale realisme hermed eksperimentelt var
tilbagevist. Mange foretrækker så at erstatte den lokale
realisme med en ikke-lokal realisme, men selv efter udelukkelse af
de mest hypotetiske forklaringsforsøg forbliver ¯ikke-lokal
realisme® en aparte størrelse, der næppe lever op til det,
EPR betegnede ¯a reasonable definition of reality®.
Den ikke-lokale realisme bygger under alle
omstændigheder på, at man vil tillægge disse
fænomener en realitet abstraheret fra målingen. Det er en
insisteren på at tale om noget uiagttageligt. Denne insistens er
forståelig, fordi vi er nødt til at tale om det, men denne
sprogbrug honorerer ikke kravet om entydighed, idet sprogbrugen bliver
paradoksal.
Samtidig må man spørge, hvad man
overhovedet skal bruge denne realisme til? Hvori består
nødvendigheden af at kræve et sådant dobbeltbogholderi,
hvor der skal være en en-til-en korrespondance mellem de
eksperimentelle resultater og en abstrakt bagvedliggende verden? Wojciech
H. Zurek skriver: ¯The only 'failure' of quantum theory is its inability
to provide a natural framework that can accomodate our prejudices about the
workings of the universe® [18].
Er det ikke disse fordomme om, hvordan universet virker,
der er den væsentligste grund til at opretholde en eller anden form
for realisme? Også selv om man må slække på en af
fysikkens grundlæggende antagelser, lokaliteten? Hvis ikke blot
realismen - eller i hvert fald naivrealismen - ikke umiddelbart kan
honoreres uden at slagte et så fundamentalt fysisk princip som
lokaliteten, men hvis den overhovedet ikke er nødvendig, hvorfor
så opretholde den som antagelse?
Iagttagelsesafhængighed og modeldannelse
Selvfølgelig er der som i al anden videnskab
mange hvis'er. Er kvantemekanikken nu også fuldstændig? Vil
fremtidige eksperimenter kunne påvise noget, der vil rokke ved vor
opfattelse af erkendelsessituationen? Der er ingen garanti for, at vi ikke
må modificere vor opfattelse, men hvor fysikken står i dag, er
der os bekendt ikke nogen overbevisende grund til ikke at antage
kvantemekanikkens fuldstændighed, og vi har vanskeligt ved at
forestille os, at de rent sproglige og begrebsmæssige overvejelser
skulle kunne ændre sig.
At vi aldrig kan iagttage noget principielt
uiagttageligt, er givet, men at vi, som det er sket så mange gange i
fysikkens historie, kan redefinere, hvad en iagttagelse er, er muligt.
Fysikere er altid underlagt muligheden af empirisk at ¯få verden i
nakken®. Dette kunne give det indtryk, at denne ¯verden® findes
derude i forvejen, og det er også den eneste måde, vi
meningsfuldt kan bruge disse begreber på, hvis vi taler fysik, men
dette gør ikke denne ¯verden® til noget abstraheret fra vort
begrebsapparat. ¯Vi hænger i sproget.® Hvis vi vil lave fysik,
må vi bruge begreberne, som begrebsrammen specificerer det, og ikke i
anden forstand. Gør vi noget andet, er det ikke længere fysik,
men metafysik. Eller i bedste fald en paradoksal sproglig støtte for
at omgås det, vi ikke kan tale entydigt om.
I en vis forstand åbner denne analyse af
begrebsapparatets rolle op for holdningen: shut up and calculate,
hvor man dropper sine erkendelsesmæssige kvaler og holder sig strengt
til at udnytte formalismen. Et særtilfælde af denne holdning
finder man hos Richard Feynman, der har dette at sige om
kvanteelektrodynamikken [19]: ¯[Physicists have] learned to realize that
whether they like a theory or they don't like a theory is not the essential
question. Rather, it is whether or not the theory gives predictions that
agree with experiment. It is not a question of whether a theory is
philosophically delightful, or easy to understand, or perfectly reasonable
from the point of view of common sense. The theory of quantum
electrodynamics describes Nature as absurd from the point of view of common
sense. And it agrees fully with experiment. So I hope you can accept Nature
as She is - absurd.®
Denne rent pragmatiske holdning understreger, at der
ikke er noget eksperimentelt grundlag for at være utilfreds med den
sædvanlige opfattelse af kvantemekanikken. Alle eksperimentelt
plausible alternativer bliver samtidig - som vi har set - nødt til
at indføre en form for ikke-lokal kausal vekselvirkning og
forudsætter altså udbredelse med mere end lysets hastighed
eller måske ligefrem tilbage i tiden, som vi blandt andet så i
diskussionen af EPRs tankeeksperiment, hvilket der ikke er det fjerneste
eksperimentelle belæg for.
Samtidig vil sådanne teorier, med deres
matematiske abstraktioner og deres brud på såvel basale fysiske
principper som almindelig hverdagsfornuft, stå den naivrealisme,
deres forfattere ofte tilstræber, fjernt.
Ophavsmænd til sådanne teorier ville, hvis
man spurgte dem, også være nødt til at indrømme,
at deres teori ikke repræsenterer et ultimativt bud på, hvordan
verden ¯virkelig® er, men blot er endnu en idealisering, endnu en -
ikke nødvendigvis uinteressant eller unyttig - model, der
først vil have bevist sit værd i det øjeblik, den
forudsiger nogle nye målbare fænomener eller mere præcist
forudsiger resultaterne af allerede kendte eksperimenter. Der er derfor
ikke meget, der taler for at betvivle standardfortolkningens
uundgåelige implikation, at der er en uløselig forbindelse
mellem iagttagelsen og det iagttagede, og at det iagttagede ikke kan
tillægges ontologisk realitet uafhængigt af iagttagelsen.
Oprindelig bragt i Faklen nr. 3, 1997
Referencer
[1] R. P. Feynman. Lectures on Physics Vol. I
(Reading, Ma.: Addison-Wesley, 1963).
[2] A. Einstein, B. Podolsky & N. Rosen. Physical
Review 47, 777 (1935).
[3] N. Bohr. Physical Review 48, 696
(1935).
[4] N. Bohr. Diskussion med Einstein om
erkendelsesteoretiske Problemer i Atomfysikken i Atomfysik og
menneskelig erkendelse (København: Schultz, 1957), s. 53.
[5] N. Bohr. Unity of Knowledge, citeret i D. Favrholdt:
Fysik, bevidsthed, liv: Studier i Niels Bohrs filosofi (Odense:
Odense Universitetsforlag, 1994), s. 83.
[6] N. Bohr. Kundskabens Enhed i Atomfysik og
menneskelig erkendelse (København: Schultz, 1957), s. 89.
[7] A. G. Zajonc, L. J. Wang, X. Y. Zou & L. Mandel.
Nature 353, 507 (1991).
[8] T. J. Herzog, P. G. Kwiat, H. Weinfurter & A.
Zeilinger. Physical Review Letters 75, 3034 (1995).
[9] N. Bohr citeret i A. Petersen. Bulletin of the
Atomic Scientists XIX no. 7 (1963), s. 10-11.
[10] ibid. s. 12.
[11] N. Bohr. Unity of Knowledge citeret i D. Favrholdt.
Fysik, bevidsthed, liv: Studier i Niels Bohrs filosofi (Odense:
Odense Universitetsforlag, 1994), s. 100.
[12] N. Bohr. Biologi og Atomfysik i Atomfysik og
menneskelig erkendelse (København: Schultz, 1957), s. 30.
[13] H. Everett. Reviews of Modern Physics
29, 454 (1957).
[14] J. S. Bell. Physics 1, 195
(1964).
[15] D. M. Greenberger, M. Horne & A. Zeilinger i M.
Kafatos red. Bell's Theorem, Quantum Theory, and Conceptions of the
Universe (Dordrecht: Kluwer, 1989).
[16] N. D. Mermin. Physics Today (June 1994), s.
9.
[17] A. Aspect, P. Grangier & G. Roger. Physical
Review Letters 47, 460 (1981); A. Aspect, J. Dalibard & G.
Roger. Physical Review Letters 49, 1804 (1982).
[18] W. H. Zurek. Physics Today (October 1991),
s. 36.
[19] R. P. Feynman. QED: The Strange Theory of Light
and Matter (Reading: Penguin, 1985), s. 10.
[ agger, Sun 27 Apr, :09:04:
/artikler/videnskabogfilosofi] -
kommentar(er) -
link
VIDENSKABELIGHED OG DANNELSE
– af Carsten Agger
De følgende overvejelser tager udgangspunkt i Thore Husfeldts glimrende
indlæg i forrige nummer af daimiposten om udviklingen indenfor teoretisk
datalogi, et emne som jeg finder yderst interessant, på trods af at min
viden om det er begrænset (omend dog naturligvis eksisterende).
Datalogien er jo generelt noget af en rodebutik, sammenstykket af
brudstykker fra forskellige discipliner, der pludselig blev relevante i
kølvandet på den rasende udvikling indenfor computerområdet.
Således har den spændende grænseområder til adskillige
discipliner: Vi kunne nævne matematik (naturligvis!), elektronik,
samfundsfag, biologi og neurologi.
Mens den teoretiske datalogi generelt har holdt den matematisk/rigoristisk
fane højt, er mange områder – og dette indbefatter en del
specialer lavet her på stedet – langt mere ingeniøragtige, og en
disciplin som (for eksempel) systemarbejde kan vel strengt taget slet ikke
kaldes videnskabelig; her drejer det sig snarere om heuristik, om en
fornuftspræget indsamling af metoder og tommelfingerregler.
Men inden for teoretisk datalogi kan vi altså spørge os selv: hvad er
formålet med forskningen? Ligger fagets berettigelse i dets rolle i
udvikling af ny teknologi? Eller er den måske snarere indhentelse af en
viden om beregnings- og beregnelighedsteori, der vil udgøre en berigelse
af vor tankeverden og indsigt i den verden, vi bebor? Spørgsmålet er
vigtigt, og rækker naturligvis langt ud over den snævre datalogiske
kontekst.
Hvis svaret er, at formålet er at udvikle teknologier, der kan sikre
økonomisk fremgang (og det synes altså at være dét, der
blæser i de bevillingspolitiske vinde), må vi spørge, hvad
formålet er med denne fremgang, specielt hvor vi vil hen med den, og
hvad den skal sætte os i stand til.
Vi kunne også reformulere spørgsmålet: hvad er værdien af de
emner, den teoretiske datalogi beskæftiger sig med, den viden, som dels
indhøstes af forskerne, dels fyldes på de studerende? Hvad er for
eksempel værdien – for nu at tage et ret basalt eksempel – af
teorien for formelle sprog? Hvis jeg skulle besvare et sådant
spørgsmål, ville jeg nok opholde mig en del ved deres relevans som
model for beregnings- og genkendelsesprocesser, deres bidrag til en
forståelse af, hvad sprog i det hele taget er eller kan være: Har vi
karakteriseret de sprog, der kan genkendes af en Turing-maskine, har vi vel
samtidig fundet nogle karakteristika for de naturlige sprog, der jo skal
genkendes af vores hjerne. Teoriens enorme praktiske betydning for
compilerteknologien bliver i denne sammenhæng en biting.
For sandheden er jo, at udvikling af teknologi ikke er, og aldrig har
været, grundforskningens målsætning. Grundforskningens formål
er at øge den menneskelige erkendelse, i stedse større detalje at
kortlægge den verden vi lever i, og den vi udspringer af. Og dette er
det egentlige formål med discipliner som fysik, matematik, biologi,
lingvistik, kulturhistorie og (klassisk, indisk, semitisk, nordisk, osv.)
filologi.
Dette er i grunden også oplagt – når Pompeji udgraves så
minutiøst, er det ikke for at fremdrage specimens, der kan tiltrække
turister, men for at øge vor viden om den klassiske kultur til gavn for
alle interesserede, i sidste ende hele menneskeheden. Dette må ikke
forstås som en nedvurdering af teknologien, kun som en konstatering af,
at videnskab er noget andet (i mine øjne: og mere) end teknologi.
Og derfor må det også skuffe, når der netop på BRICS lægges
op til, at ph.d.-projekter bør indeholde en praktisk anvendelse eller
dimension, for netop her skulle man forvente, at forskning i og udvidelse
af datalogiens matematiske grundlag havde allerhøjeste prioritet.
Bevægelsen hen mod demo or die er kortsynet, kontraproduktiv og til
syvende og sidst udtryk for en deintellektualisering af
universitetsmiljøet.
Det er til gengæld – som Thore rigtigt påpeger – også
forfejlet at sige, at grundforskerne blot skal have lov at gøre deres
arbejde, så skal de nok af sig selv finde frem til noget, der er pengene
værd. Ikke fordi dette aldrig er sket – faktisk skyldes alle
teknologiske fremskridt af nogen betydning opdagelser, der er gjort helt
uden skelen til deres praktiske nytte – men fordi det ikke og aldrig er
derfor, videnskaben er værd at støtte.
Det har at gøre med det andet hovedpunkt i Thores artikel, teoretisk
datalogi og videnskaben generelt som en del af vor kulturelle baggrund, en
dannelseskultur, der ansås for en selvfølge i begyndelsen af dette
århundrede, og som vi måske ligefrem gjorde klogt i at genindføre.
Når Bohr udover sit engagement i fysikken svor til Goethes digtning og
fik aftenerne til at gå med at udrede Kierkegaard, og når Heisenberg
udviklede kvantemekanikken på grundlag af en skarpsindig og vidende
filosofisk analyse af den eksperimentelle problemstilling, er det ikke et
udtryk for disse fysikeres geni, men for tidens generelle akademiske
niveau. Vi skal ikke langt tilbage i tiden, før ingen filosoffer kunne
tages alvorligt, hvis de ikke havde et vue over samtidens videnskab og
matematik, og hvor ingen videnskabsfolk kunne tages alvorligt uden en vis
filosofisk indsigt.
Hvorfor har man hørt om ubestemthedsrelationerne og ikke om Turings
halting-teorem i gymnasiet? Og hvorfor gør man ikke mere ud af den
tværvidenskabelige relevans af kompleksitetsteorien, herunder et begreb
som NP-fuldstændighed? Måske fordi fagudviklingen på gymnasiet
er gået i stå, eller måske fordi gymnasiet har andre problemer end
almen dannelse at slås med i en tid, hvor op mod halvdelen af de
studerende, der begynder på universitetet har svært ved at skrive en
sammenhængende sætning på deres eget modersmål (og det kan jeg
personligt bevidne efter flere års erfaring med at rette obligatoriske
Dat1-opgaver).
Dette kunne tyde på, at det måske var på tide at genindføre den
ovennævnte dannelseskultur, ikke for at gøre universitetet til et
elitært elfenbenstårn, men tværtimod for at indføre det
stænk af tværfaglig indsigt, der igen ville forvandle universitetet
til det, navnet siger: Universitas, hvor al viden og al kundskab forener
sig. En sådan forening, et sådant bredt udsyn er til syvende og sidst
også forudsætningen for ethvert videnskabeligt gennembrud. Og det er
værd at være opmærksom på, at netop den teoretiske datalogi –
som ovenfor antydet – ville have en hel del at bidrage med i den
sammenhæng.
Dette svarer også godt til det krav om rehabilitering af
dannelsesidealet, først og fremmest en styrkelse af studenternes
kendskab til grundlaget for deres fag, der så skarpt og velformuleret
blev fremsat i første nummer af tidsskriftet Faklen, og som ligger bag
overvejelserne om at indføre et studieforberende Studium Generale.
Det skal blive spændende at se, om disse tanker har en chance, eller om
de vil blive begravet i en dyne af erhvervsrettethed og økonomiske
hensyn.
Oprindelig bragt i daimiposten, december 1996
[ agger, Thu 29 Dec, :12:21:
/artikler/videnskabogfilosofi] -
kommentar(er) -
link
|
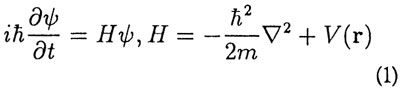
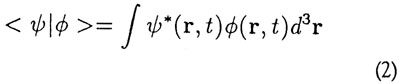
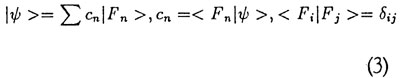

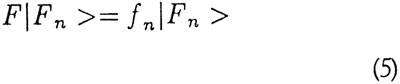
![]() sætter dette os i stand til at komme med mangfoldige forudsigelser om mikroskopiske systemer, som bekendt med stor succes.
sætter dette os i stand til at komme med mangfoldige forudsigelser om mikroskopiske systemer, som bekendt med stor succes.