EINSTEIN-PODOLSKY-ROSEN-PARADOKSET
- af Carsten Agger
oprindelig bragt i Tidsskriftet Elsebeth nr. 11, 1995
Denne artikel omhandler det såkaldte Einstein-Podolsky-Rosen-Paradoks, med hovedvægten lagt på gennemgangen af forfatterens oprindelige argument og af Bohrs svar herpå.
Einstein, Podolsky og Rosen beviste i deres artikel fra 1935, at kvantemekanikken i følge sin egen formalisme er ufuldstændig: den samme fysiske virkelighed kan beskrives af to forskellige bølgefunktioner, der er egenfunktioner for to ikke-kommuterende observable. Dette er i modstrid med kvantemekanikken, der derfor må afløses af en mere fuldstændig teori.
Denne holdning deles stadig af mange mennesker, også (en minoritet blandt) fysikere. I artiklen gennemgås omhyggeligt EPR's oprindelige argument og Niels Bohrs tilbagevisning heraf. Bohr viste ved et eksempel, at de omtalte to forskellige bølgefunktioner repræsenterer to forskellige måleprocedurer, der gensidigt udelukker hinanden.
EPR-paradokset hører til de emner fra fysikken, der oftest behandles i den populærvidenskabelige litteratur, og er vel det, der oftest misforstås. Specielt går forfatterne som regel let hen over Bohrs svar eller slår det direkte hen som "uforståeligt". Dette er, som vi skal se, ikke rigtigt.
1. Kvantemekanikkens grundbegreber og fortolkning
1.1 Formalismen
I ikke-relativistisk kvantemekanik beskrives en partikel ved en bølgefunktion ψ (r,t), der opfylder Schrödingers ligning:
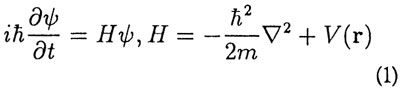
Bølgefunktionen kan også opfattes som en vektor | ψ > i et Hilbertrum. Fysiske størrelser repræsenteres så af observable, der er hermiteske mht. skalarproduktet
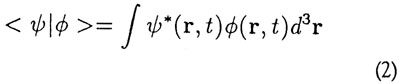
Et vigtigt postulat er det, at en måling af en fysisk størrelse kun kan resultere i en egenværdi for dennes repræsenterende operator. Antag, at vi ønsker at måle en given størrelse F (repræsenteret ved operatoren F), mens vores partikel er i tilstanden | ψ >. Hvad er vi nu i stand til at sige om resultatet af denne måling? For at svare på dette spørgsmål opløses | ψ > i egenvektorer for F:
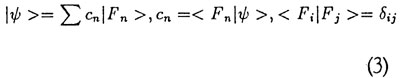
hvor vores | Fn > opfylder

Den almindelige fysiske fortolkning af ovenstående bygger på følgende regler:
Sandsynligheden for at få værdien fn som resultat af målingen er givet ved | cn | 2 = | < Fn | ψ > | 2 Dette kaldes Borns fortolkning.
Men hvordan ser bølgefunktionen nu ud efter målingen? Ja, vores måling gav resultatet fk, og målinger postuleres nu (ideelt set) at kunne gentages med samme resultat, så vores system efter målingen beskrives af en tilstand ψ', der opfylder
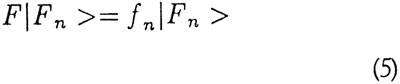
dvs. tilstanden er blevet projiceret ind på egenvektoren hørende til den målte egenværdi. Denne opførsel kaldes reduktion af bølgepakken eller (mere farverigt) "collapse of the wave function".
Et systems tilstand er fuldstændigt beskrevet ved dets bølgefunktion.
Suppleret med den sædvanlige kvantisering ![]() sætter dette os i stand til at komme med mangfoldige forudsigelser om mikroskopiske systemer, som bekendt med stor succes.
sætter dette os i stand til at komme med mangfoldige forudsigelser om mikroskopiske systemer, som bekendt med stor succes.
En i denne sammenhæng specielt relevant konsekvens af den matematiske formalisme er, at to operatorer kun kan have fælles egentilstande, hvis de kommuterer, og det vil i følge fortolkningen sige, at de tilhørende fysiske størrelser ikke samtidig kan have en bestemt værdi; dette udtrykkes mest præcist ved ubestemtheds-relationen:
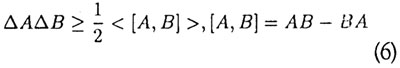
Som vi senere skal se, sætter disse relationer grænser ikke (alene) for den nøjagtighed hvormed sådanne par af fysiske størrelser kan kendes, men også for den nøjagtighed, hvormed de overhovedet kan defineres.
2. EPRs argument
EPR søger i deres artikel at vise, at kvantemekanikken ikke kan give en fuldstændig beskrivelse af den fysiske virkelighed. De mener, at man i hvert fald må stille to krav til en fysisk teori:
Korrekthed, det vil sige overensstemmelse mellem teoriens forudsigelser og de erfaringer, man kan gøre (via observationer, eksperimenter, ...)
Fuldstændighed, det vil sige, at "alt hvad der findes i den fysiske virkelighed skal også findes i teorien".
Det sidste punkt udtrykker EPR som, at hvert element af den fysiske virkelighed skal have sit modstykke i teorien, hvor et sådant element defineres ved følgende kriterium:
Hvis man uden på nogen måde at forstyrre et system med sikkerhed (det vil sige, med sandsynlighed een) kan forudsige værdien af en fysisk størrelse, så findes der et element af fysisk virkelighed svarende til denne størrelse.
Kvantemekanikkens ufuldstændighed bliver nu en konsekvens af følgende argumentation: Hvis to fysiske størrelser (fx A og B) repræsenteres af operatorer, der ikke kommuterer, har de ingen fælles egentilstande. Dette betyder, at hvis det betragtede system er i en egentilstand for A ("værdien af A er kendt"), har det ingen mening (i kvanteteorien) at tillægge det nogen værdi for B. Dette vil også sige: Kan vi i en given tilstand forudsige værdien af to ikke-kommuterende operatorer, må kvanteteorien være ufuldstændig. EPR udtrykker det præcist ved to punkter:
Kvantemekanikkens beskrivelse af virkeligheden er ufuldstændig, eller
hvis operatorene svarende til to fysiske størrelser ikke kommuterer, kan de to størrelser ikke samtidig være veldefinerede.
Antag, at vi har en situation, hvor et system, der (i een dimension) beskrives af bølgefunktionen ψ(χ1, χ2, t), splittes i to systemer (1) og (2), så det samlede system stadig er beskrevet ved ψ. Ønsker man nu at måle en fysisk størrelse A i systemet (1), må vi opløse ψ i egenvektorer for A(l) efter forskriften (3):
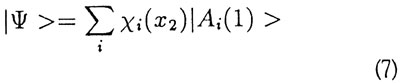
Måler vi i stedet en anden størrelse B i systemet (1), fås tilsvarende
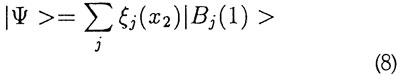
Måler vi altså A i system l (det vil sige A(l)) får vi et resultat ak, måler vi B(l), kan vi få resultatet bl. Samtidig vil system 2's tilstand efter målingen være enten | χk > eller | ξ1 >. Nu kan tilsyneladende den samme fysiske tilstand (system 2 efter målingen) beskrives ved to forskellige bølgefunktioner. Lader man specielt de to systemer være to partikler, A være deres position χ, B deres impuls ρ, kan man vælge
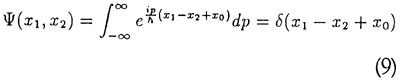
hvor δ er Diracs deltafunktion, defineret ved
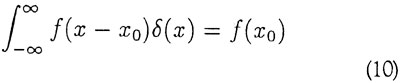
Måles nu χ1 med resultatet χ' + χ0 fås jf. (7)
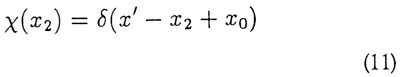
så partikel 2 nu er i en egentilstand for χ med værdien χ' + χ0. Vælger vi i stedet at måle ρ1 med resultatet ρ' fås omvendt
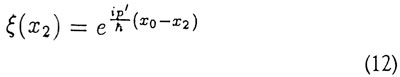
svarende til egenværdien -ρ' for ρ2. Da målingerne på partikel l i følge EPR ikke medfører nogen påvirkning af system 2, konkluderer EPR, at der i denne situation findes et element af fysisk virkelighed svarende til såvel ρ2 som χ2. Men så må - som ovenfor anført - den kvantemekaniske beskrivelse være ufuldstændig og bør afløses af en mere fuldstændig teori.
3. Bohrs argument
Det fortælles, at Niels Bohr efter offentliggørelsen af EPRs artikel straks lagde alt andet arbejde til side for at rette denne misforståelse. Kort efter kom der da også et svar, hvor han imødegik argumentet ved et eksempel, hvor det viser sig, at de to bølgefunktioner, der tilsyneladende begge beskriver et systems tilstand, er udtryk for to hinanden gensidigt udelukkende eksperimentelle procedurer; selv om der ikke kan være tale om, at målingen på eet system direkte, mekanisk påvirker det andet system, påvirker den selve de betingelser, der overhovedet tillader os at definere de pågældende fysiske størrelser. Denne formulering fandt fysikeren J.S. Bell (der er kendt for at have opstillet Bells ulighed) så kringlet og kryptisk, at han flot imødegik hele Bohrs argumentation ved at håne denne ene sætning. Lad i stedet os andre, der ønsker at gennemgå denne argumentation, begynde med at betragte konsekvenserne af at bruge det samme måleinstrument til at måle to ikke-kommuterende fysiske størrelser.
3.1 Målinger - et eksempel
Fysiske størrelser skal kunne defineres operationelt, dvs. som målelige størrelser. Lad os for at belyse problemerne i forbindelse med valget af måleprocedure se på en meget simpel kollision: En partikel passerer igennem en enkelt spalte i en skærm (Fig.l).
Dette simple eksempel illustrerer alle problemer ved måling af position og impuls. Skærmen betragtes i det følgende som et enkelt måleinstrument, der kan indgå i en større eksperimental opstilling. Det kan antages, at partiklens impuls før den passerer gennem spalten er fuldstændig kendt. Diffraktionen i spalten vil give en usikkerhed Δρ i partiklens impuls umiddelbart efter kollisionen; denne usikkerhed er forbundet med usikkerheden Δχ på partiklens stedkoordinat ved usikkerhedsrelationen, i dette tilfælde skrevet og fortolket som en ubestemthedsrelation:

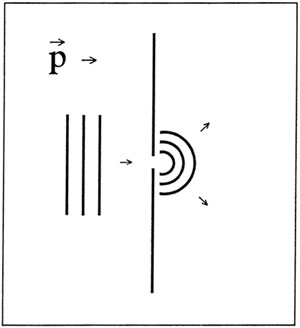
Figur 1.
Den således introducerede usikkerhed Δρ er forbundet med en udveksling af impuls mellem partiklen og skærmen. I hvilken udstrækning er det nu muligt at tage denne udveksling i betragtning? Vi ser på to mulige tilfælde:
Skærmen antages først at være spændt fast til resten af opstillingen på et fast underlag, der definerer koordinatsystemet (Fig.2). Den udvekslede impuls vil nu absorberes af dette underlag, og vi er således helt afskåret fra at tage den i betragtning ved forudsigelser om eksperimentets videre forløb.
Nu tænkes skærmen ikke fastspændt til underlaget, men i stedet ophængt på en sådan måde, at dens impuls kan måles før og efter partiklen passerer (Fig.3). Det er nu muligt ved impulsbevarelse at forudsige partiklens impuls efter kollisionen; omvendt må vi opgive en nøjagtig bestemmelse af skærmens (og dermed partiklens) position, idet den passerer.
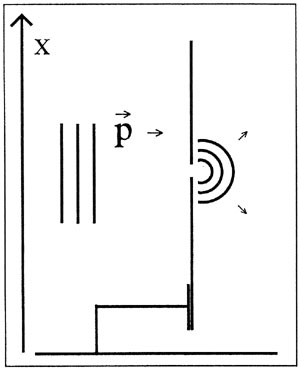
Figur 2: Opstilling, der muliggør kontrol af partiklens begyndelsesposition
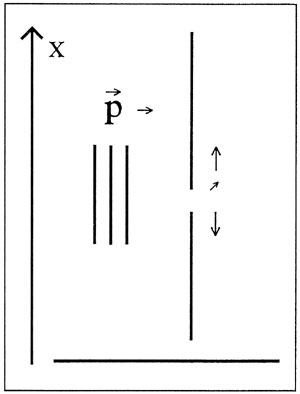
Figur 3: Opstilling, der muliggør forudsigelse af partiklens impuls
Skærmen kan bruges til at fastlægge begyndelsesbetingelserne for en partikel i forbindelse med en opstilling som i figur 4, hvor partiklen sendes ind mod en skærm med flere spalter for til sidst at blive registreret på en fotografisk plade.
I tilfældet 1) ovenfor kan skærmen bruges til at fastlægge begyndelsespositionen; gentages eksperimentet et stort antal gange, vil der på den fotografiske plade dannes et interferensmønster ud fn de sædvanlige betingelser.
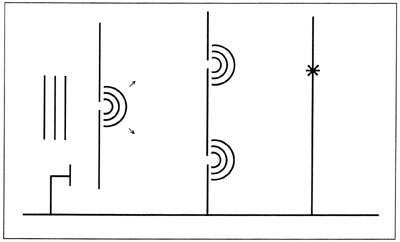
Figur 4: Skærm som før, her brugt til at kontrollere begyndelsesbetingelserne i et dobbeltspalteeksperiment
I tilfælde 2) kan skærmen derimod ikke bruges til at måle position med, eftersom en nøjagtig måling af skærmens impuls betyder, at relationen (13) må tages i betragtning ved overvejelser over dens position. Især gælder det, at hvis partiklens impuls kendes med tilstrækkelig nøjagtighed til at forudsige, hvilken spalte den vil passere igennem, vil usikkerheden på dens begyndelsesposition fuldstændig ødelægge interferensmønstret.
Desuden gælder i tilfælde 2), at efter den første måling af skærmens impuls kan man frit vælge, om man (efter kollisionen med partiklen) vil måle dens position (og herved fastlægge partiklens begyndelsesposition) eller dens impuls (og herved fastlægge partiklens impuls).
Men nu må vi ikke tabe ubestemthedsrelationen (13) af syne; for måler vi skærmens position, vil den herved udvekslede impuls som før absorberes af underlaget, og vi er helt afskåret fra at forudsige noget om partiklens impuls; for denne kan vi kun her definere (som målelig størrelse) ud fra impulsbevarelsessætningen, og absorptionen af en ukontrollabel impuls i vores underlag (id est, vores referencesystem) ødelægger hele grundlaget for at bruge denne på skærmpartikel-systemet. Omvendt vil målingen af skærmens impuls, som vi har set, fjerne ethvert grundlag for en meningsfuld definition af partiklens position i forhold til vort referencesystem. Bohr kaldte dette forhold komplementaritet: at størrelser som position og impuls, der er nødvendige for at beskrive alle aspekter af fysiske systemer og processer, dog ikke kan defineres samtidigt.
Man kan sætte situationen på spidsen ved at antage, at vi har 1000 fuldstændig identiske sådanne systemer. Straks efter, at alle partikler har ramt deres fotografiske plade, har vi to muligheder: Enten måler vi alle skærmenes impulser, og er nu i stand til at sige, hvilken spalte samtlige partikler passerede igennem; eller vi kan måle positionen af hver enkelt skærm og dermed kende hver enkelts begyndelsesposition. I det første tilfælde kan vi sortere alle disse stykker fotopapir (som vi i mellemtiden har fået fremkaldt) efter, hvilket hul partiklen passerede igennem, og kan betragte fordelingen svarende til partikler, der er blevet skudt ind mod et enkelt hul. I det andet tilfælde kan vi sortere dem efter begyndelsespositionen og vil herved få et interferensmønster svarende til diffraktion af bølger i begge spalter; vi har nu ingen ret til at tale om, hvorvidt en partikel er gået igennem den ene eller den anden spalte.
Det skulle nu være slået fast, at den måling, der i vores opstilling tillader os at bestemme partiklens impuls, langt fra at indebære nogen mekanisk forstyrrelse (her: forskydning) af partiklen påvirker det grundlag, hvorpå vi ville bygge en forudsigelse af dens position. Hvad mere er, det er netop denne påvirkning, der i kvanteteorien udtrykkes (eller: tages højde for) ved de tilsvarende operatorers manglende kommuteren.
3.2 EPRs eksempel
Man kan begynde med at bemærke, at EPR i deres eksempel udnytter, at
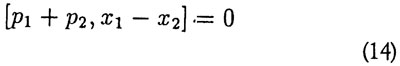
det vil sige, de opstiller en tilstand, der er egentilstand for både χ1 - χ2 og ρ1 + ρ2. Nøjagtig det samme kunne opnås ved en opstilling som i fig.5: to partikler sendes ind mod en skærm med to spalter, der er meget smalle i forhold til afstanden mellem dem. Hvis vi måler skærmens impuls både før og efter kender vi både
summen af deres impulser - fra målingen på skærmen
deres indbyrdes afstand - som jo er afstanden mellem spalterne.
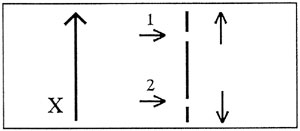 |
| Fig. 5. |
Præcis som før kan vi nu måle den ene partikels position, det vil sige den kan fastlægges i forhold til et instrument, der er fastspændt til det underlag, der definerer vort koordinatsystem. En sådan måling vil også fortælle os om skærmens placering ved kollisionen, og ud fra afstanden mellem spalterne kan vi forudsige den anden partikels position. Men: ved målingen har vi absorberet en helt ukontrollabel impuls i underlaget, hvilket forhindrer os i at bruge impulsbevarelsessætningen på systemet bestående af skærmen og de to partikler. Dette betyder så ikke, at den anden partikels impuls ikke kan måles, men at vi ikke kan definere den uden at foretage en ny i måling; i et grundlag, vores definition, hvile på, er væk. Omvendt vil en måling af den ene partikels impuls nok tillade forudsigelse af den andens impuls, men dette vil medføre en ukontrollabel forskydning af såvel partikel som måleapparat, der fjerner et hvert grundlag for at anstille forudsigelser vedrørende dens position; vi har ikke fastlagt de betingelser, der kunne tillade os overhovedet meningsfuldt at tale om, at den har en position.
For at opsummere kan vi med Bohr konstatere, at disse eksempler på ubestemthedsrelationernes rolle i forbindelse med målinger viser, hvor EPR går galt i byen med deres kriterium for fysisk virkelighed: Umuligheden af i den samme tilstand at give en præcis forudsigelse af målinger på to ikke-kommuterende størrelser repræsenterer ikke en arbitrær udelukkelse af en del af virkeligheden, men afspejler derimod umuligheden af at tilvejebringe omstændigheder, hvorunder begge kan defineres. Det er derfor meningsløst at søge efter en "mere fuldstændig" teori.
4. Realismen og den moderne fysik
EPRs artikel er blot eet af mange lignende angreb på kvanteteorien. De har alle deres udspring i en filosofisk indstilling, der kaldes realisme. Realismen er en doktrin, der (meget groft sagt) går ud på følgende: Verden består af virkelige genstande (real af latin res, ting) med visse egenskaber (attributter). Disse genstande eksisterer uafhængigt af vor sansning af dem, er "objektivt virkelige". Genstandenes attributter opdeles gerne i primære og sekundære: de primære attributter er egenskaber, som genstandene besidder uafhængigt af vore sansninger eller begreber, mens de sekundære er mindre "virkelige" i og med at de ikke kan gives nogen mening uden at referere til en menneskelig iagttager. Et oplagt eksempel på det sidste er en egenskab som "skønhed": en æstetisk vurdering kræver naturligvis en iagttager til at foretage denne vurdering. Men hvilke attributter er nu primære? Forskellige tiders realister har givet forskellige svar:
Anaxagoras mente, at det skulle være størrelse, farve og smag
Empedokles anså farve og smag i for antropomorfe, og foretrak størrelse, form og position
Den Newtonske fysik er kompatibel med en realisme hvor man anser masse, position og hastighed for primære
Men hvad med kvantefysikken?
I følge den sædvanlige fortolkning er kvantemekanikken ikke forenelig med forestillingen om en verden bestående af genstande med objektive egenskaber; de attributter, vi kan udpege, er ikke uafhængige af iagttagelsen, de kan faktisk kun defineres i forbindelse med en bestemt iagttagelsesprocedure. Jagten på primære attributter har visse mindelser om selskabslegen "Jerusalem brænder". Man har ofte hørt den indvending, at selv om vi efter at have målt en partikels impuls har mistet al information om dens position, må den dog stadig være eet eller andet sted, dvs. den må have een eller anden position, som vi blot ikke kender. Men det er netop ikke rigtigt. Position kan kun defineres i forbindelse med eet eller andet referencesystem, en bestemt eksperimentel procedure.
Men hvis (dogmatisk) realisme ikke umiddelbart er foreneligt med kvantefysikken, hvad er så alternativerne?
Heisenberg gør sig til talsmand for en pragmatisk realisme: det vi forstår som objektive egenskaber ved genstandene kan fortsat betragtes som sådan (en klassisk partikel kan fx som sædvanligt siges "virkelig" at have både position og impuls), hvis blot vi husker, at alle sådanne egenskaber er menneskeskabte begreber, som kun kan have begrænset anvendelsesområde. Denne indstilling er i virkeligheden slet ikke realisme i streng forstand, men måske snarere et forslag om en rationel udnyttelse af vort begrebsapparat. Niels Bohr ligger med sit tidligere nævnte komplementaritetsprincip ikke så langt herfra. Her pointeres det, at forskellige klassiske begreber (som position og impuls), som hver for sig er nødvendige for at kunne give en udtømmende beskrivelse af fysiske fænomener, dog ikke kan defineres samtidig. Herved afslører de sig netop også som dele, ikke af en præeksisterende ydre verden, men af et begrebsapparat. Den klassiske fysik er netop en forfinelse af vores sædvanlige (hverdags-)begreber, som netop ikke slår til i den moderne fysik. Komplementaritetsprincippet bygger på den observation, at vi ikke kan undvære de klassiske begreber (da de netop er afledt af vores hverdagssprog), og repræsenterer på en måde en umiddelbar generalisering af disse.
Henry Margeneau foreslår, at man simpelthen afskaffer realismen; det lykkes ham at opbygge en sammenhængende og rationel definition af (fysisk) virkelighed uden overhovedet at referere til en "ydre" verden. Et sådant synspunkt kunne forekomme ekstremt, men det er det i filosofisk forstand i virkeligheden slet ikke - tilfældet er snarere, at et langt mere ekstremt synspunkt (metafysisk realisme) i århundreder - siden Descartes og Locke - har været sat i forbindelse med en helt enestående succesrig videnskab og teknologi (nemlig den klassiske naturvidenskab).
5. Referencer
Jeg har ikke forsøgt at henvise hver eneste gang, jeg bruger en reference. Hovedparten af artiklen er naturligvis skrevet på baggrund af
A. Einstein, B. Podolsky, N. Rosen, Phys Rev 47, 777 (1935)
N. Bohr, Phys Rev 48, 696 (1935)
Begge artikler kan desuden sammen med mange andre spændende artikler om beslægtede emner findes i den i høj grad anbefalelsesværdige
J.A. Wheeler & W.H. Zurek, Quantum Theory and Measurement, Princeton University Press 1983
En grundig behandling af den moderne fysiks erkendelsesteoretiske virkninger findes i bøgerne
Petersen, A., Quantum Physics and the Philosophical Tradition, MIT Press 1968
Margeneau, H., The Nature of Physical Reality, McGraw-Hill 1950
Disse være hermed også anbefalet til alle interesserede.
